Thread Rating:
Is this correct?
What is the correct formula to work this out?
Also what is the probability of not seeing a streak of 6 either player/banker in 65 hands? 130 hands? 200 hands?
Quote: DanthemanAs far as I can work out the probability of hitting exactly 6 banker or player in a row in baccarat is approx 1/65?
Is this correct?
What is the correct formula to work this out?
Also what is the probability of not seeing a streak of 6 either player/banker in 65 hands? 130 hands? 200 hands?
Is this the baccarat playing high roller "Dan the Man" from the BBC Louis Theroux documentary about Vegas?
(Fast forward to the final 10mins.)
For baccarat, if you ignore ties, the probability of the player winning is about 49.3176%, and the banker, about 50.6824%.
The probability of going a particular number of spins without a run of 6 wins in a row is:
68.65%, for 65 spins
45.91%, for 130 spins
29.77%, for 200 spins
For the player in baccarat, if you ignore ties (i.e. determine the probability of going through N non-tied hands without the player winning 6 times in a row):
62.74% for 65 hands
38.12% for 130 hands
22.29% for 200 hands
For the banker:
58.35% for 65 hands
32.82% for 130 hands
17.66% for 200 hands
why 00 roulette? (and not 0 roulette)Quote: ThatDonGuyFor even-money bets on double-zero roulette tables, the probability of a single win is 9/19, so the probability of N wins in a row is (9/19)N. For N = 6, this is about 1 / 88.525.
and you did not point out that
6 in a row is the very next 6 spins/bets
it is at least 3 times more likely in the very next 10 spins
0.035077761
RIGHT!?
streaks RULE in gambling
cuz
all wins and losses are in streaks (length >=1)
ok
maybe after lunch i looks at your others
remember the prob of a win in a Bac shoe changes as the cards are used up
maybe a simulation would be more accurate per shoe that is
here is an accurate streak calculator i found
http://maxgriffin.net/CalcStreaks.shtml
Sally
AhhhQuote: DanthemanAlso what is the probability of not seeing a streak of 6 either player/banker in 65 hands? 130 hands? 200 hands?
you used the word
EITHER
so Dons answers are not correct, in my opinion, as i read the question differently as written
either
they are close
how close you wants?
this is like asking the chance of a run of 3 Heads or Tails in 9 flips (or = either)
not just Heads, not just Tails
like here
https://wizardofvegas.com/forum/off-topic/general/14542-please-help-a-probability-math-question/
using the streak calculator i linked tooooooooooooooooooooooooo
instead of 6 for the streak (K)
use 5
instead of 65 hands
use 64 (N)
streak length -1
AND
hands -1
for EITHER run of banker or player
i knew
i knew
it was easy
==============================
edit: i think that method only works for 50/50 bets
so i will see later
easy to simulate too
================================
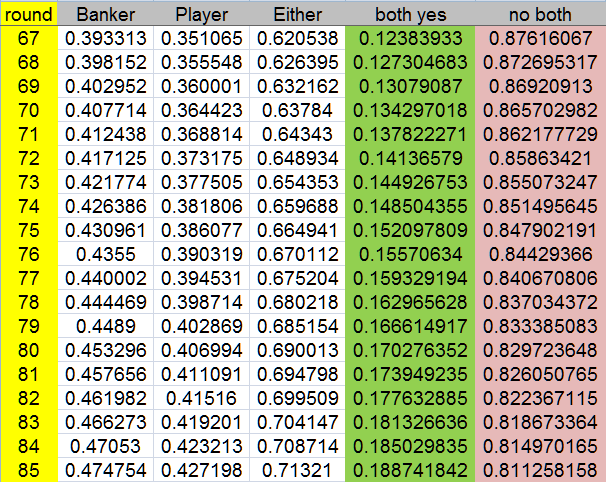
nows if you just want the NO Banker prob of at least a 6 run in N hands
Don be rights
all in the way the question is interpreted
trick trick
Mully
Banker 6 in a Row win is 1 in 107.5 (75.3% chance this will happen in any 1 shoe)
Player 6 in a Row win is 1 in 126.6 (64% chance this will happen in any 1 shoe)
Banker 6 wins BEFORE a LOSS: 1 in 34.68 (will happen twice in a standard shoe)
Player 6 wins BEFORE a LOSS: 1 in 39.7 (will happen twice in a standard shoe
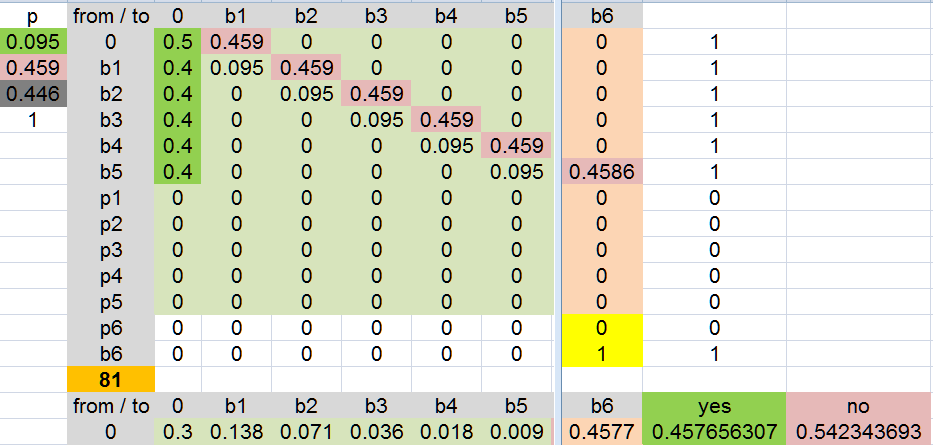
Formula: chance of a win ^ 6, Banker 1/(0.4586^6), and Player 1/(0.44625^6)
chance in any 1 shoe (standard rules, 8 decks) 81/chance of a win (81 is the average # of rounds in a standard shoe)
6 BEFORE a LOSS adds the chance of a tie (0.09516) to the chance of a win.
HUH?Quote: 98ClubsBaccarat: 8 decks (standard game)
Banker 6 in a Row win is 1 in 107.5 (75.3% chance this will happen in any 1 shoe)
by these sim data from me Dad
https://wizardofvegas.com/forum/gambling/tables/5928-baccarat-streaks-question/
the chance of NO 6 run or longer in an 8 deck shoe (13 or 14 card ribbon) is about 56.44%
so 43.56% chance there is at least 1 such run
(a tie does not break the streak)
you say different
"75.3% chance this will happen in any 1 shoe"
"some ONE IS way off!"
says Bill Clinton
streak probabilities are challenging to calculate (computers calculate)
easy to do something different (like the number of runs per N trials)
Sally
added:
OK
i say now 98Clubs is way off (way way off) and my Dad is about 2% off (could not find his sim data either)
here what i gots
Don, finish your homework, please. (trash goes out tonight)
thank you
my sim data
8 deck,13 card ribbon
group middle freq freq/100
--------------------------------------------
-0.5 <= x < 0.50 0.00 544738 54.47% <<< no run of 6 Banker
0.50 <= x < 1.50 1.00 349382 34.94%
1.50 <= x < 2.50 2.00 93018 9.30%
2.50 <= x < 3.50 3.00 11887 1.19%
3.50 <= x < 4.50 4.00 937 0.09%
4.50 <= x < 5.50 5.00 38 0.00%
this is close to me calculated value in Excel
i C Sally says
automate R code next project
Quote: 98ClubsFormula: chance of a win ^ 6, Banker 1/(0.4586^6), and Player 1/(0.44625^6)
chance in any 1 shoe (standard rules, 8 decks) 81/chance of a win (81 is the average # of rounds in a standard shoe)
Not quite. You are assuming that each group of 6 hands (hands 1-6, hands 2-7, hands 3-8, ..., hands 76-81) is independent of the others. If hands 1-5 are player wins and hand 6 is a bank win, then none of the groups 1-6, 2-7, 3-8, 4-9, 5-10, and 6-11 have player wins.
looks to me You are assumingQuote: ThatDonGuyNot quite. You are assuming <snip>
we have to each assume, i assume, what exactly the OP wants...
exactly...
exact
either
a Banker / Player run per N hands played
and the run = exactly 6 and no more, no no more than 6
BBB BBB P = counts as an OP success
but this does not count as an OP success
BBB BBB BB P
what really is OP after?
i knows streaks are in the OPs blood
he said in another thread
streaks rule!
Sally
yepQuote: mustangsallyusing the streak calculator i linked tooooooooooooooooooooooooo
instead of 6 for the streak (K)
use 5
instead of 65 hands
use 64 (N)
streak length -1
AND
hands -1
for EITHER run of banker or player
i knew
i knew
it was easy
==============================
edit: i think that method only works for 50/50 bets
so i will see later
easy to simulate too
================================
i was 1st wrong
i knew it after reading
ok
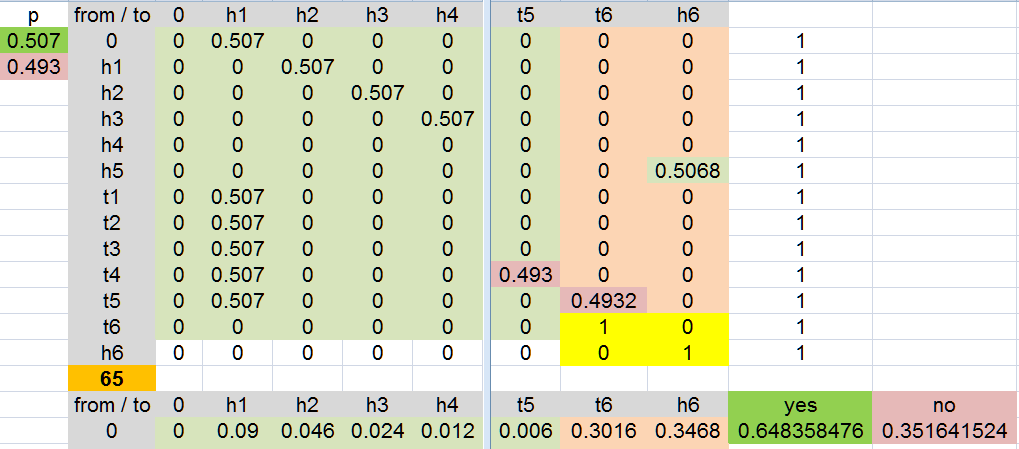
the probability of NO Banker or Player run of 6 or longer in 65 Banker/Player hands
is abouts
[1] 0.3516415
that means the prob of 1 or the other (either) is abouts
[1] 0.6483585
> ##############################################
> # Biased/unbiased recursion of heads OR tails
> ##############################################
>
> N = 65 # number of flips
> m = 6 # length of run (must be > 1 and <= N/2)
> p = 0.506825 # P(heads)
>
> prob = rep(0,N)
> h = rep(0,N)
> t = rep(0,N)
>
> h[m] = p^m
> t[m] = (1-p)^m
> prob[m] = h[m] + t[m]
>
> for (n in (m+1):(2*m-1)) {
+ h[n] = (1-p)*p^m
+ t[n] = p*(1-p)^m
+ prob[n] = prob[n-1] + h[n] + t[n]
+ }
>
> for (n in (2*m):N) {
+ h[n] = ((1-p) - t[n-m] - prob[n-m-1]*(1-p))*p^m
+ t[n] = (p - h[n-m] - prob[n-m-1]*p)*(1-p)^m
+ prob[n] = prob[n-1] + h[n] + t[n]
+ }
>
> # m heads OR m tails
> prob[N]
[1] 0.6483585
> 1-prob[N]
[1] 0.3516415
that was using BruceZ code (R code)
from that same link (hey, He is no longer over at 2+2. maybe he is about to release his own website!)
but I had to check this in Excel using transition matrix (sure)
yep
right on!
oh yes
130

200

simulation time too?
Sally is good
"be good"
added for fun B4 dinner
for no run of 6 either B or P
in Baccarat (Tie does not break the streak) and counting all hands - Ties included
me matrix shows:
65 hands played
B or P run

130 hands played
B or P run

200 hands played
B or P run

Could anyone answer my question in other post about whether some streaks of different lengths are more reliable (hit to consistantly closer to expected probability) than others.
For example i found streaks of 2 would usually hit with in 3 of expected (expect 24 hit 21-27 times) over a shoe, where streaks of 3 or more werent as reliable (would swing more wildly)
For longer streaks which happen less often, they will tend to be farther from expectation for longer, compared to shorter streaks, since they happen less often.
Worded another way, the more frequently something happens, the more quickly it will show the expected results.
too addQuote: DanthemanThanks.
Could anyone answer my question in other post about whether some streaks of different lengths are more reliable (hit to consistantly closer to expected probability) than others.
the variance for smaller streaks is smaller than the larger ones (the wait time - how long do we have to wait)
you seem to be attracted to the length of streaks
where 3
say BBBP
is NOT a streak of length 2 or longer
but exactly length 3
is this right?
that is ok too
as an example because in an 8 deck shoe your values look to be way off to meQuote: DanthemanFor example i found streaks of 2 would usually hit with in 3 of expected (expect 24 hit 21-27 times) over a shoe, where streaks of 3 or more werent as reliable (would swing more wildly)
unless streaks of 2 for you are >=2 not just =2
here is a streaks summary of 1000 8 deck shoes (13 card ribbon)
----------------------- frequencies [37172 streaks] ------------------------
length 1 2 3 4 5 6 7 8 9 10 11 12 13
player 9514 4693 2243 1114 537 257 111 59 36 17 5 1 1
banker 9202 4701 2344 1151 628 287 158 80 43 12 10 6 3
--------------------------------------------------------------------
length 14 15 16 17
player 2 1 1 1
banker 1 0 0 1
have fun with streaks!
i do
Sally
here is a larger sim sample
1 million 8 deck shoes
P and B streaks
group middle freq freq/100
-----------------------------------------------
0.50 <= x < 1.50 1.00 18949473 50.66%
1.50 <= x < 2.50 2.00 9348285 24.99%
2.50 <= x < 3.50 3.00 4612786 12.33%
3.50 <= x < 4.50 4.00 2275990 6.09%
4.50 <= x < 5.50 5.00 1123300 3.00%
5.50 <= x < 6.50 6.00 553106 1.48%
6.50 <= x < 7.50 7.00 273695 0.73%
7.50 <= x < 8.50 8.00 134253 0.36%
8.50 <= x < 9.50 9.00 66125 0.18%
9.50 <= x < 10.50 10.00 32767 0.09%
10.50 <= x < 11.50 11.00 16235 0.04%
11.50 <= x < 12.50 12.00 7947 0.02%
12.50 <= x < 13.50 13.00 4050 0.01%
13.50 <= x < 14.50 14.00 1863 0.00%
14.50 <= x < 15.50 15.00 892 0.00%
15.50 <= x < 16.50 16.00 467 0.00%
16.50 <= x < 17.50 17.00 264 0.00%
17.50 <= x < 18.50 18.00 143 0.00%
18.50 <= x < 19.50 19.00 60 0.00%
19.50 <= x < 20.50 20.00 36 0.00%
20.50 <= x < 21.50 21.00 8 0.00%
21.50 <= x < 22.50 22.00 4 0.00%
22.50 <= x < 23.50 23.00 3 0.00%
23.50 <= x < 24.50 24.00 2 0.00%
24.50 <= x < 25.50 25.00 1 0.00%
-----------------------------------------------
cumulative
-----------------------------------------------
0.50 <= x < 1.50 1.00 18949473 50.66%
1.50 <= x < 2.50 2.00 28297758 75.66%
2.50 <= x < 3.50 3.00 32910544 87.99%
3.50 <= x < 4.50 4.00 35186534 94.08%
4.50 <= x < 5.50 5.00 36309834 97.08%
5.50 <= x < 6.50 6.00 36862940 98.56%
6.50 <= x < 7.50 7.00 37136635 99.29%
7.50 <= x < 8.50 8.00 37270888 99.65%
8.50 <= x < 9.50 9.00 37337013 99.83%
9.50 <= x < 10.50 10.00 37369780 99.91%
10.50 <= x < 11.50 11.00 37386015 99.96%
11.50 <= x < 12.50 12.00 37393962 99.98%
12.50 <= x < 13.50 13.00 37398012 99.99%
13.50 <= x < 14.50 14.00 37399875 99.99%
14.50 <= x < 15.50 15.00 37400767 100.00%
15.50 <= x < 16.50 16.00 37401234 100.00%
16.50 <= x < 17.50 17.00 37401498 100.00%
17.50 <= x < 18.50 18.00 37401641 100.00%
18.50 <= x < 19.50 19.00 37401701 100.00%
19.50 <= x < 20.50 20.00 37401737 100.00%
20.50 <= x < 21.50 21.00 37401745 100.00%
21.50 <= x < 22.50 22.00 37401749 100.00%
22.50 <= x < 23.50 23.00 37401752 100.00%
23.50 <= x < 24.50 24.00 37401754 100.00%
24.50 <= x < 25.50 25.00 37401755 100.00%
Only P streaks
group streak freq freq/100
-----------------------------------------------
0.50 <= x < 1.50 1.00 9591472 51.31%
1.50 <= x < 2.50 2.00 4674314 25.00%
2.50 <= x < 3.50 3.00 2273436 12.16%
3.50 <= x < 4.50 4.00 1107294 5.92%
4.50 <= x < 5.50 5.00 538186 2.88%
5.50 <= x < 6.50 6.00 261965 1.40%
6.50 <= x < 7.50 7.00 127691 0.68%
7.50 <= x < 8.50 8.00 61671 0.33%
8.50 <= x < 9.50 9.00 29881 0.16%
9.50 <= x < 10.50 10.00 14511 0.08%
10.50 <= x < 11.50 11.00 7095 0.04%
11.50 <= x < 12.50 12.00 3395 0.02%
12.50 <= x < 13.50 13.00 1748 0.01%
13.50 <= x < 14.50 14.00 766 0.00%
14.50 <= x < 15.50 15.00 372 0.00%
15.50 <= x < 16.50 16.00 185 0.00%
16.50 <= x < 17.50 17.00 92 0.00%
17.50 <= x < 18.50 18.00 57 0.00%
18.50 <= x < 19.50 19.00 22 0.00%
19.50 <= x < 20.50 20.00 12 0.00%
20.50 <= x < 21.50 21.00 3 0.00%
21.50 <= x < 22.50 22.00 1 0.00%
22.50 <= x < 23.50 23.00 0
23.50 <= x < 24.50 24.00 2 0.00%
24.50 <= x < 25.50 25.00 1 0.00%
-----------------------------------------------
cumulative
-----------------------------------------------
0.50 <= x < 1.50 1.00 9591472 51.31%
1.50 <= x < 2.50 2.00 14265786 76.31%
2.50 <= x < 3.50 3.00 16539222 88.47%
3.50 <= x < 4.50 4.00 17646516 94.40%
4.50 <= x < 5.50 5.00 18184702 97.27%
5.50 <= x < 6.50 6.00 18446667 98.68%
6.50 <= x < 7.50 7.00 18574358 99.36%
7.50 <= x < 8.50 8.00 18636029 99.69%
8.50 <= x < 9.50 9.00 18665910 99.85%
9.50 <= x < 10.50 10.00 18680421 99.93%
10.50 <= x < 11.50 11.00 18687516 99.96%
11.50 <= x < 12.50 12.00 18690911 99.98%
12.50 <= x < 13.50 13.00 18692659 99.99%
13.50 <= x < 14.50 14.00 18693425 100.00%
14.50 <= x < 15.50 15.00 18693797 100.00%
15.50 <= x < 16.50 16.00 18693982 100.00%
16.50 <= x < 17.50 17.00 18694074 100.00%
17.50 <= x < 18.50 18.00 18694131 100.00%
18.50 <= x < 19.50 19.00 18694153 100.00%
19.50 <= x < 20.50 20.00 18694165 100.00%
20.50 <= x < 21.50 21.00 18694168 100.00%
21.50 <= x < 22.50 22.00 18694169 100.00%
22.50 <= x < 23.50 23.00 18694169 100.00%
23.50 <= x < 24.50 24.00 18694171 100.00%
24.50 <= x < 25.50 25.00 18694172 100.00%
only B streaks
group streak freq freq/100
-----------------------------------------------
0.50 <= x < 1.50 1.00 9358001 50.02%
1.50 <= x < 2.50 2.00 4673971 24.98%
2.50 <= x < 3.50 3.00 2339350 12.50%
3.50 <= x < 4.50 4.00 1168696 6.25%
4.50 <= x < 5.50 5.00 585114 3.13%
5.50 <= x < 6.50 6.00 291141 1.56%
6.50 <= x < 7.50 7.00 146004 0.78%
7.50 <= x < 8.50 8.00 72582 0.39%
8.50 <= x < 9.50 9.00 36244 0.19%
9.50 <= x < 10.50 10.00 18256 0.10%
10.50 <= x < 11.50 11.00 9140 0.05%
11.50 <= x < 12.50 12.00 4552 0.02%
12.50 <= x < 13.50 13.00 2302 0.01%
13.50 <= x < 14.50 14.00 1097 0.01%
14.50 <= x < 15.50 15.00 520 0.00%
15.50 <= x < 16.50 16.00 282 0.00%
16.50 <= x < 17.50 17.00 172 0.00%
17.50 <= x < 18.50 18.00 86 0.00%
18.50 <= x < 19.50 19.00 38 0.00%
19.50 <= x < 20.50 20.00 24 0.00%
20.50 <= x < 21.50 21.00 5 0.00%
21.50 <= x < 22.50 22.00 3 0.00%
22.50 <= x < 23.50 23.00 3 0.00%
-----------------------------------------------
cumulative
-----------------------------------------------
0.50 <= x < 1.50 1.00 9358001 50.02%
1.50 <= x < 2.50 2.00 14031972 75.01%
2.50 <= x < 3.50 3.00 16371322 87.51%
3.50 <= x < 4.50 4.00 17540018 93.76%
4.50 <= x < 5.50 5.00 18125132 96.89%
5.50 <= x < 6.50 6.00 18416273 98.44%
6.50 <= x < 7.50 7.00 18562277 99.22%
7.50 <= x < 8.50 8.00 18634859 99.61%
8.50 <= x < 9.50 9.00 18671103 99.80%
9.50 <= x < 10.50 10.00 18689359 99.90%
10.50 <= x < 11.50 11.00 18698499 99.95%
11.50 <= x < 12.50 12.00 18703051 99.98%
12.50 <= x < 13.50 13.00 18705353 99.99%
13.50 <= x < 14.50 14.00 18706450 99.99%
14.50 <= x < 15.50 15.00 18706970 100.00%
15.50 <= x < 16.50 16.00 18707252 100.00%
16.50 <= x < 17.50 17.00 18707424 100.00%
17.50 <= x < 18.50 18.00 18707510 100.00%
18.50 <= x < 19.50 19.00 18707548 100.00%
19.50 <= x < 20.50 20.00 18707572 100.00%
20.50 <= x < 21.50 21.00 18707577 100.00%
21.50 <= x < 22.50 22.00 18707580 100.00%
22.50 <= x < 23.50 23.00 18707583 100.00%
Quote: ThatDonGuyNot quite. You are assuming that each group of 6 hands (hands 1-6, hands 2-7, hands 3-8, ..., hands 76-81) is independent of the others. If hands 1-5 are player wins and hand 6 is a bank win, then none of the groups 1-6, 2-7, 3-8, 4-9, 5-10, and 6-11 have player wins.
All I did was take the chance of a win and raise it to the 6th power. Then inverted the fraction for 1 in x analysis.
For 6 Before a loss the chance of a tie was added to the chance of a win, then raised to the 6th power. Again the fraction was inverted for '1 in x' analysis.
Streak analysis involves "less than, greater than, or equal to" phrasing. The OP wanted to know the chance of 6 Banker wins and 6 Player wins in a row... nothing else. The simple math used does not presume when the streak starts. It only states the probabiliity of the occurance based upon winning percentage. In fact, neither 6 consecutive or 6 before a loss presumes such will occur in one shoe ( hands 79, 80, 81, Shuffle/cut/burn. 1, 2, and 3).
I made no assumption, just did the easy math of chance ^6.
that appears to me to be your opinionQuote: 98ClubsThe OP wanted to know the chance of 6 Banker wins and 6 Player wins in a row... nothing else.
OP used the word either and or
that means, to me, one or the other and not both
but we may never really know
OP seems happy :)
my Excel shows this (as well as a few sims)
example 1
Banker run of 6 in 81 hands (Ties do NOT break the run): 0.457656307
Player run of 6 in 81 hands (Ties do NOT break the run): 0.411091138
Either (NOT both): 0.694798211
Banker AND Player 6 run: 0.173949235
example 2
Banker run of 6 in 74 hands (Ties do NOT break the run): 0.426386042
Player run of 6 in 74 hands (Ties do NOT break the run): 0.381806137
Either (NOT both): 0.659687823
Banker AND Player 6 run: 0.148504355
ask not for my workbooks
Sally
So the variance on shorter streaks is less, does this include streaks of 1 or more?
As the simple banker/ player appears to be have a higher variance at a glance?
Quote: sisyphusWhat role does probability play in games of chance? Assuming, Banker/Player is 50/50, what difference does it make if we have a 10 in a row banker run? Apparently probability never changes even after a banker run of 23. It's always 50/50? But why do streaks end?
Why do streaks end? Well, that's like asking "why did the coin I flipped land on tails?" It's just probability/statistics/math.


