November 9th, 2013 at 6:33:30 PM
permalink
I want to compare the odds between 2 different pay tables that have the same top prize to see which has a better return.
The Keno offered at my local casino has the option of picking 1-15 or 20 numbers (you can't pick 16-19 numbers). 20 numbers are drawn on a video screen by a random number generator (no physical balls are used)
The paytable for a $1 bet picking 15 is
0 - $10
1 - $2
6 - $1
7 - $5
8 - $20
9 - $50
10 - $250
11 - $2000
12 - $10000
13 - $25000
14 - $50000
15 - $100000
The paytable for a $1 bet picking 20 is
0 - $200
1 - $2
2 - $1
7 - $1
8 - $2
9 - $5
10 - $10
11 - $20
12 - $200
13 - $1000
14 - $4000
15 - $8000
16 - $10000
17 - $50000
18 - $65000
19 - $80000
20 - $100000
My question is, how does the return on picking 20 numbers compare to picking 15? I can't use the calculator on the site cause it only goes up to 15 not 20.
The Keno offered at my local casino has the option of picking 1-15 or 20 numbers (you can't pick 16-19 numbers). 20 numbers are drawn on a video screen by a random number generator (no physical balls are used)
The paytable for a $1 bet picking 15 is
0 - $10
1 - $2
6 - $1
7 - $5
8 - $20
9 - $50
10 - $250
11 - $2000
12 - $10000
13 - $25000
14 - $50000
15 - $100000
The paytable for a $1 bet picking 20 is
0 - $200
1 - $2
2 - $1
7 - $1
8 - $2
9 - $5
10 - $10
11 - $20
12 - $200
13 - $1000
14 - $4000
15 - $8000
16 - $10000
17 - $50000
18 - $65000
19 - $80000
20 - $100000
My question is, how does the return on picking 20 numbers compare to picking 15? I can't use the calculator on the site cause it only goes up to 15 not 20.
November 9th, 2013 at 6:54:36 PM
permalink
If I figured this out right, it's 70.0234% return for 15/15, and 68.6954% return for 20/20.
November 9th, 2013 at 8:14:50 PM
permalink
I basically agree. I also get 70.0234% for the 15-spot game, but 68.6915% 68.69615% for the 20-spot game.
November 9th, 2013 at 9:09:19 PM
permalink
Now I'm getting 68.69615% for 20...
November 9th, 2013 at 9:25:20 PM
permalink
Here's the one I use for non-standard games which Wizard's doesn't calculate:
http://betstarter.com/lottery/KenoOdds.asp
It's a bit of a pain because it doesn't explicitly give you the probability of zero, so you have to do 1 - (Sum of All Other Probabilities). Further, you can't put the pays in there, but you just multiply the probability of each event by the pay for each and sum those up. It's time-consuming, but very easy, should you ever need to determine a similar problem.
http://betstarter.com/lottery/KenoOdds.asp
It's a bit of a pain because it doesn't explicitly give you the probability of zero, so you have to do 1 - (Sum of All Other Probabilities). Further, you can't put the pays in there, but you just multiply the probability of each event by the pay for each and sum those up. It's time-consuming, but very easy, should you ever need to determine a similar problem.
https://wizardofvegas.com/forum/off-topic/gripes/11182-pet-peeves/120/#post815219
November 9th, 2013 at 11:22:13 PM
permalink
Quote: ThatDonGuyNow I'm getting 68.69615% for 20...
Yup, that's actually what I got too but I accidentally omitted one of the sixes in my original post.
November 9th, 2013 at 11:58:29 PM
permalink
Quote: Mission146Here's the one I use for non-standard games which Wizard's doesn't calculate:
http://betstarter.com/lottery/KenoOdds.asp
It's a bit of a pain because it doesn't explicitly give you the probability of zero, so you have to do 1 - (Sum of All Other Probabilities). Further, you can't put the pays in there, but you just multiply the probability of each event by the pay for each and sum those up. It's time-consuming, but very easy, should you ever need to determine a similar problem.
There is actually an easier way to calculate zero hits... in keno 80C20 its simply 80C20/60C20. Using words...
f=field (80)
d=draw (20)
C=combination function (found on some calculators as nCr)
so the regular keno is as I wrote above but getting there illustrates a universal method. Since zero matches means all 20 draws missed, the formula for zero hits becomes fCd/(f-d)Cd or 80C20/(80-20)C20 = 80C20/60C20 ~= 843.38 for 1.
Another example for f=64 and d=16 yields 64C16/(64-16)C16 = 64C16/48C16 ~= 216.66 for 1. And so on.
Some people need to reimagine their thinking.
November 10th, 2013 at 12:16:04 AM
permalink
It's only easier if you know how to do it.
But, now I do! Thanks 98Clubs!
But, now I do! Thanks 98Clubs!
https://wizardofvegas.com/forum/off-topic/gripes/11182-pet-peeves/120/#post815219
November 10th, 2013 at 2:02:27 AM
permalink
Thank you, here a bonus answer.
Suppose we were looking for zero hits when we select 15 numbers in regular keno. To answer this we need one more variable p= number of picks. This will also open the gate to figuring out "partials" such as 7 of 10.
If we picked 15 numbers, the odds are 80C15/(80-20)C15. fCp/(f-d)Cp.
Partials need one more variable m = match. If we wish to figure the odds of correctly matching 7 of 10 picks from a field of 80 having 20 drawn...
80C10/(20C7*60C3) or fCp/(pCm*(f-d)C(p-m)). Solving the numeric at left, is ~ 620.68 for 1.
With much thanks to CASIO for their model FX-260 handheld calc.
Suppose we were looking for zero hits when we select 15 numbers in regular keno. To answer this we need one more variable p= number of picks. This will also open the gate to figuring out "partials" such as 7 of 10.
If we picked 15 numbers, the odds are 80C15/(80-20)C15. fCp/(f-d)Cp.
Partials need one more variable m = match. If we wish to figure the odds of correctly matching 7 of 10 picks from a field of 80 having 20 drawn...
80C10/(20C7*60C3) or fCp/(pCm*(f-d)C(p-m)). Solving the numeric at left, is ~ 620.68 for 1.
With much thanks to CASIO for their model FX-260 handheld calc.
Some people need to reimagine their thinking.
November 13th, 2013 at 9:50:53 AM
permalink
Thanks everyone! Basically I wanted to know which $1 bet with a slim chance of big payoff was better :)
November 26th, 2013 at 2:21:38 PM
permalink
I also get very hungry this time of year.Quote: JBI basically agree. I also get 70.0234% for the 15-spot game, but 68.6915% 68.69615% for the 20-spot game.
can your (JB) calculator be updated to include pick 20? (I am sure it can be, I could try to look at it too)
It would be interesting to see what it returns and how close it is to other calculations. (how large the error is)
I think I did this correctly
the *totals combos* and a few other combos are slightly off
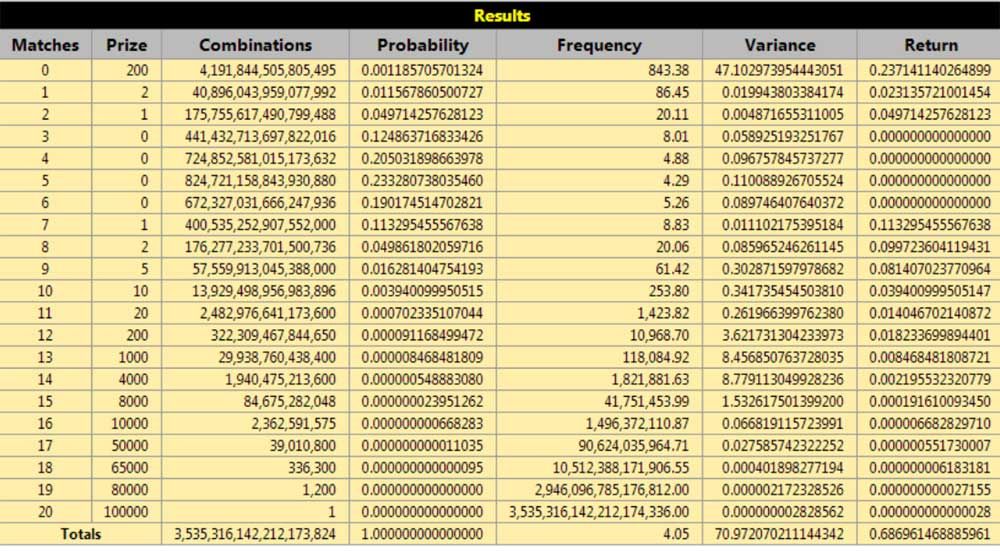
the *totals combos* and a few other combos are slightly off

That brings up what exactly is 80choose20 or C(80,20) for pick 20 calculations to start with
80! / (20! * (80-20)!)
Wolfram Alpha
http://www.wolframalpha.com/input/?i=80%21+%2F+%2820%21+*+60%21%29
3,535,316,142,212,174,320
3.53531614221217432 × 10^18
Here is what I also found
Excel 2007
3,535,316,142,212,180,000
Windows 7 calculator
3,535,316,142,212,174,320
http://en.wikipedia.org/wiki/Keno
3,535,316,142,212,174,336 to be exact
and
3,535,316,142,212,173,800.000 (to not be exact)
http://www.picalc.com/
3,535,316,142,212,172,300
http://www.mathproblems.info/gam470/games/keno/prob-keno.html
3,535,316,142,212,180,000 <<<< matches my Excel
http://www.lotto-logix.com/kenocomp.html
3,535,316,142,212,174,320 <<<< matches Windows 7 calc (looks to be the most accurate site I found)
http://betstarter.com/lottery/KenoOdds.asp
3,535,316,142,212,170,000
R program
require(Rmpfr)
chooseZ(80,20)
Big Integer ('bigz') :
3,535,316,142,212,174,320<<<< matches Windows 7 calc
Sally
I Heart Vi Hart


