October 27th, 2013 at 8:35:49 AM
permalink
The Georgia Lottery's Keno game is standard Keno (20 numbers picked from 1-80). However, there are two wrinkles: (1) for double the bet, you can buy a "Multiplier". (2) Sometimes they run a "30% more" promotion where for a limited time (usually Monday 6-8PM) all winnings are increased 30%.
I THINK I have calculated the returns for all the applicable betting combinations (excluding the max payout limits)... Any corrections or feedback would be greatly appreciated.
Does this look right to you?
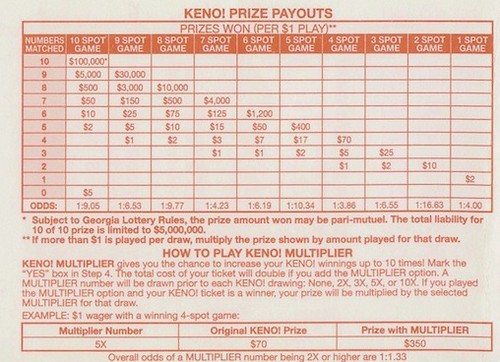
Pay Table and Rules:

Base Game Return (7 spot):
This portion was as simple as using The Wizards Keno Calculator:
Multiplier Wheel weights:
The wheel is made up of 5 "1x" spots, 6 "2x" spots, 4 "3x" spots, 2 "5x" spots and 1 "10x" spot. I calculated the natural wheel probabilities and then downloaded 10098 trials to get the actual wheel weights (I suspected that the wheel was not naturally weighted.) Here are the results:
According to the 10098 trials downloaded, the wheel is not weighted naturally.
Per the official Keno rules, the overall odds of a Multiplier being 2x or greater are 1 in 1.33. The 10098 sample produced odds of 1 in 1.32069 (pretty close). I wonder if the wheel weights change slightly during the 30% promo, or if 10k samples is not enough to get closer to the 1 in 1.33 number stated by the Georgia Lottery.
Base Game Return with Multiplier and 30% Promotion (7 spot):
To calculate the impact that the Multiplier has on the return, I created a table of all possible outcomes of matched numbers and multiplier results. I then calculated returns based on the combined probability of multiplier and numbers matched. Finally, since the multiplier costs and additional $1 to play, I divide the overal return by 2 in order to get the return per dollar bet and overall house edge.
For the 30% promo, I simply added 30% to the return of each possible combination.
Provided the approach above is correct, here are the overall results for all of the games offered:
I THINK I have calculated the returns for all the applicable betting combinations (excluding the max payout limits)... Any corrections or feedback would be greatly appreciated.
Does this look right to you?
Pay Table and Rules:


Base Game Return (7 spot):
This portion was as simple as using The Wizards Keno Calculator:
| Match | Collect ($) | Frequency | Probability (%) | Return |
|---|---|---|---|---|
| 0 | 0 | 386206920 | 12.1574251954 | 0 |
| 1 | 0 | 1001277200 | 31.519250506592 | 0 |
| 2 | 0 | 1037687280 | 32.665405070468 | 0 |
| 3 | 1 | 555903900 | 17.499324144894 | 0.1749932414 |
| 4 | 3 | 165795900 | 5.219096674793 | 0.1565729002 |
| 5 | 15 | 27442080 | 0.863850484104 | 0.1295775726 |
| 6 | 125 | 2325600 | 0.073207668144 | 0.0915095852 |
| 7 | 4000 | 77520 | 0.002440255605 | 0.0976102242 |
| Total | 3176716400 | 100 | 0.650263523681 | |
| House Edge: | 34.974% |
Multiplier Wheel weights:
The wheel is made up of 5 "1x" spots, 6 "2x" spots, 4 "3x" spots, 2 "5x" spots and 1 "10x" spot. I calculated the natural wheel probabilities and then downloaded 10098 trials to get the actual wheel weights (I suspected that the wheel was not naturally weighted.) Here are the results:
| Multiplier | Trial Count | Trial Probability | # of Spots | Natural Probability |
|---|---|---|---|---|
| Mult x1 | 2452 | 0.242820360467419 | 5 | 0.277777777777778 |
| Mult x2 | 5167 | 0.511685482273718 | 6 | 0.333333333333333 |
| Mult x3 | 1740 | 0.172311348781937 | 4 | 0.222222222222222 |
| Mult x5 | 623 | 0.061695385224797 | 2 | 0.111111111111111 |
| Mult x10 | 116 | 0.0114874232521291 | 1 | 0.0555555555555556 |
| Grand Total | 10098 | 1 | 18 | 1 |
According to the 10098 trials downloaded, the wheel is not weighted naturally.
Per the official Keno rules, the overall odds of a Multiplier being 2x or greater are 1 in 1.33. The 10098 sample produced odds of 1 in 1.32069 (pretty close). I wonder if the wheel weights change slightly during the 30% promo, or if 10k samples is not enough to get closer to the 1 in 1.33 number stated by the Georgia Lottery.
Base Game Return with Multiplier and 30% Promotion (7 spot):
To calculate the impact that the Multiplier has on the return, I created a table of all possible outcomes of matched numbers and multiplier results. I then calculated returns based on the combined probability of multiplier and numbers matched. Finally, since the multiplier costs and additional $1 to play, I divide the overal return by 2 in order to get the return per dollar bet and overall house edge.
For the 30% promo, I simply added 30% to the return of each possible combination.
| Numbers Matched | Collect ($) | Multiplier | Collect Incl. Multiplier ($) | Base Probability | Multiplier Probability | Total Probability | Total Return | Total Return: +30% Promo |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0.121574251954 | 0.242820360467419 | 0.0295207036830271 | $0.00 | $0.00 |
| 0 | 0 | 2 | 0 | 0.121574251954 | 0.511685482273718 | 0.0622077797431489 | $0.00 | $0.00 |
| 0 | 0 | 3 | 0 | 0.121574251954 | 0.172311348781937 | 0.0209486233313488 | $0.00 | $0.00 |
| 0 | 0 | 5 | 0 | 0.121574251954 | 0.061695385224797 | 0.00750057030771856 | $0.00 | $0.00 |
| 0 | 0 | 10 | 0 | 0.121574251954 | 0.0114874232521291 | 0.00139657488875659 | $0.00 | $0.00 |
| 1 | 0 | 1 | 0 | 0.31519250506592 | 0.242820360467419 | 0.0765351576967356 | $0.00 | $0.00 |
| 1 | 0 | 2 | 0 | 0.31519250506592 | 0.511685482273718 | 0.161279428963716 | $0.00 | $0.00 |
| 1 | 0 | 3 | 0 | 0.31519250506592 | 0.172311348781937 | 0.0543112456738662 | $0.00 | $0.00 |
| 1 | 0 | 5 | 0 | 0.31519250506592 | 0.061695385224797 | 0.0194459230200107 | $0.00 | $0.00 |
| 1 | 0 | 10 | 0 | 0.31519250506592 | 0.0114874232521291 | 0.00362074971159108 | $0.00 | $0.00 |
| 2 | 0 | 1 | 0 | 0.32665405070468 | 0.242820360467419 | 0.079318254340253 | $0.00 | $0.00 |
| 2 | 0 | 2 | 0 | 0.32665405070468 | 0.511685482273718 | 0.167144135471488 | $0.00 | $0.00 |
| 2 | 0 | 3 | 0 | 0.32665405070468 | 0.172311348781937 | 0.0562862000620066 | $0.00 | $0.00 |
| 2 | 0 | 5 | 0 | 0.32665405070468 | 0.061695385224797 | 0.0201530474934656 | $0.00 | $0.00 |
| 2 | 0 | 10 | 0 | 0.32665405070468 | 0.0114874232521291 | 0.00375241333746711 | $0.00 | $0.00 |
| 3 | 1 | 1 | 1 | 0.17499324144894 | 0.242820360467419 | 0.0424919219679937 | $0.04 | $0.06 |
| 3 | 1 | 2 | 2 | 0.17499324144894 | 0.511685482273718 | 0.089541501145442 | $0.18 | $0.23 |
| 3 | 1 | 3 | 3 | 0.17499324144894 | 0.172311348781937 | 0.03015332146179 | $0.09 | $0.12 |
| 3 | 1 | 5 | 5 | 0.17499324144894 | 0.061695385224797 | 0.0107962754429283 | $0.05 | $0.07 |
| 3 | 1 | 10 | 10 | 0.17499324144894 | 0.0114874232521291 | 0.002010221430786 | $0.02 | $0.03 |
| 4 | 3 | 1 | 3 | 0.05219096674793 | 0.242820360467419 | 0.0126730293588755 | $0.04 | $0.05 |
| 4 | 3 | 2 | 6 | 0.05219096674793 | 0.511685482273718 | 0.0267053599907461 | $0.16 | $0.21 |
| 4 | 3 | 3 | 9 | 0.05219096674793 | 0.172311348781937 | 0.00899309587456904 | $0.08 | $0.11 |
| 4 | 3 | 5 | 15 | 0.05219096674793 | 0.061695385224797 | 0.00321994179876811 | $0.05 | $0.06 |
| 4 | 3 | 10 | 30 | 0.05219096674793 | 0.0114874232521291 | 0.000599539724971269 | $0.02 | $0.02 |
| 5 | 15 | 1 | 15 | 0.00863850484104 | 0.242820360467419 | 0.00209760485940088 | $0.03 | $0.04 |
| 5 | 15 | 2 | 30 | 0.00863850484104 | 0.511685482273718 | 0.0044201975157114 | $0.13 | $0.17 |
| 5 | 15 | 3 | 45 | 0.00863850484104 | 0.172311348781937 | 0.00148851242061889 | $0.07 | $0.09 |
| 5 | 15 | 5 | 75 | 0.00863850484104 | 0.061695385224797 | 0.000532955883934236 | $0.04 | $0.05 |
| 5 | 15 | 10 | 150 | 0.00863850484104 | 0.0114874232521291 | 0.000099234161374593 | $0.01 | $0.02 |
| 6 | 125 | 1 | 125 | 0.00073207668144 | 0.242820360467419 | 0.000177763123677053 | $0.02 | $0.03 |
| 6 | 125 | 2 | 250 | 0.00073207668144 | 0.511685482273718 | 0.000374593009803969 | $0.09 | $0.12 |
| 6 | 125 | 3 | 375 | 0.00073207668144 | 0.172311348781937 | 0.000126145120390731 | $0.05 | $0.06 |
| 6 | 125 | 5 | 625 | 0.00073207668144 | 0.061695385224797 | 4.51657528755318E-05 | $0.03 | $0.04 |
| 6 | 125 | 10 | 1250 | 0.00073207668144 | 0.0114874232521291 | 8.40967469271539E-06 | $0.01 | $0.01 |
| 7 | 4000 | 1 | 4000 | 0.00002440255605 | 0.242820360467419 | 5.9254374563874E-06 | $0.02 | $0.03 |
| 7 | 4000 | 2 | 8000 | 0.00002440255605 | 0.511685482273718 | 1.24864336611557E-05 | $0.10 | $0.13 |
| 7 | 4000 | 3 | 12000 | 0.00002440255605 | 0.172311348781937 | 4.20483734670232E-06 | $0.05 | $0.07 |
| 7 | 4000 | 5 | 20000 | 0.00002440255605 | 0.061695385224797 | 1.50552509597445E-06 | $0.03 | $0.04 |
| 7 | 4000 | 10 | 40000 | 0.00002440255605 | 0.0114874232521291 | 2.80322489780154E-07 | $0.01 | $0.01 |
| Return per 2$ bet: | $1.43 | $1.87 | ||||||
| Return per 1$ bet: | $0.72 | $0.93 | ||||||
| House Edge: | 28.260% | 6.739% |
Provided the approach above is correct, here are the overall results for all of the games offered:
| Probability of a Win | Probability of a Jackpot Win (1:n) | House Edge | House Edge w/ Multiplier | HE after 30% Promo (no Multiplier) | HE after 30% Promo w/ Multiplier | |
|---|---|---|---|---|---|---|
| 1 Spot | 25.00% | 4.00 | 50.00% | 44.84% | 35.00% | 28.29% |
| 2 Spot | 6.01% | 16.67 | 39.87% | 33.67% | 21.84% | 13.77% |
| 3 Spot | 15.26% | 72.07 | 37.56% | 31.11% | 18.83% | 10.45% |
| 4 Spot | 25.89% | 326.44 | 35.67% | 30.32% | 16.37% | 9.41% |
| 5 Spot | 9.67% | 1550.57 | 36.86% | 30.34% | 17.92% | 9.44% |
| 6 Spot | 16.16% | 7752.84 | 36.09% | 29.49% | 16.91% | 8.33% |
| 7 Spot | 23.66% | 40979.31 | 34.97% | 28.26% | 15.47% | 6.74% |
| 8 Spot | 10.23% | 230114.64 | 35.28% | 28.60% | 15.86% | 7.17% |
| 9 Spot | 15.31% | 1380687.64 | 37.16% | 30.68% | 18.31% | 9.88% |
| 10 Spot | 5.90% | 8911710.79 | 36.33% | 29.76% | 17.23% | 8.68% |
October 27th, 2013 at 9:02:52 AM
permalink
I am not a mathematician, so the value of my feedback is limited, but it appears to me your approach is logical and correct. On the base game, your return goes from .65...to .845... with the 30% bonus, not counting the wheel multipliers. So I think you're in the ballpark of knowing your risk. So this moves their keno from a complete sucker bet into the range of a return comparable to slots. Still not a great bet, let alone at a +ev.
If the House lost every hand, they wouldn't deal the game.


