February 3rd, 2023 at 8:03:25 AM
permalink
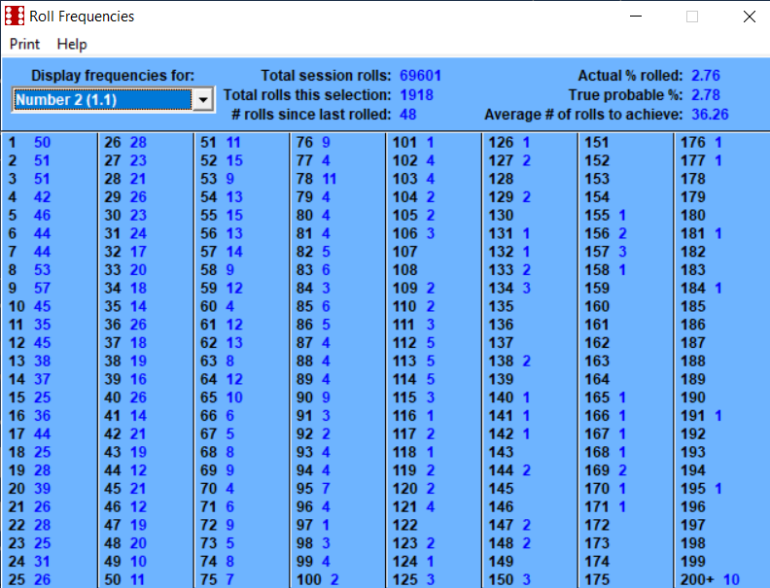
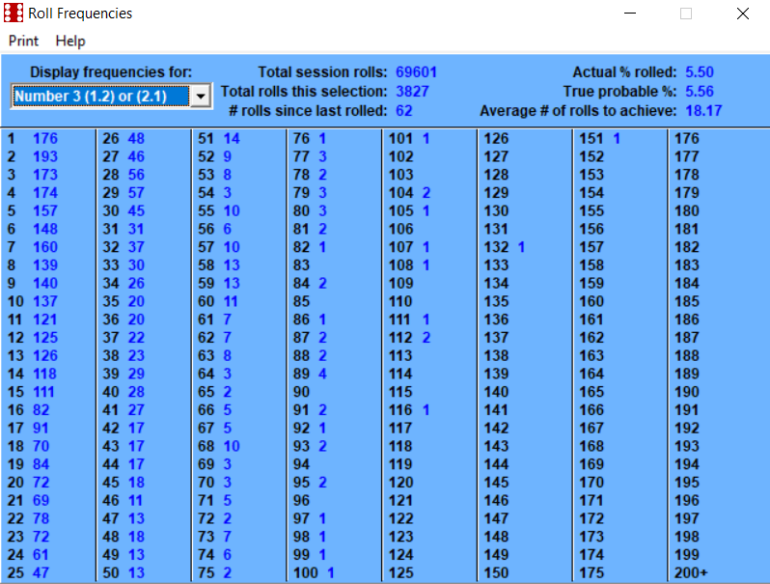
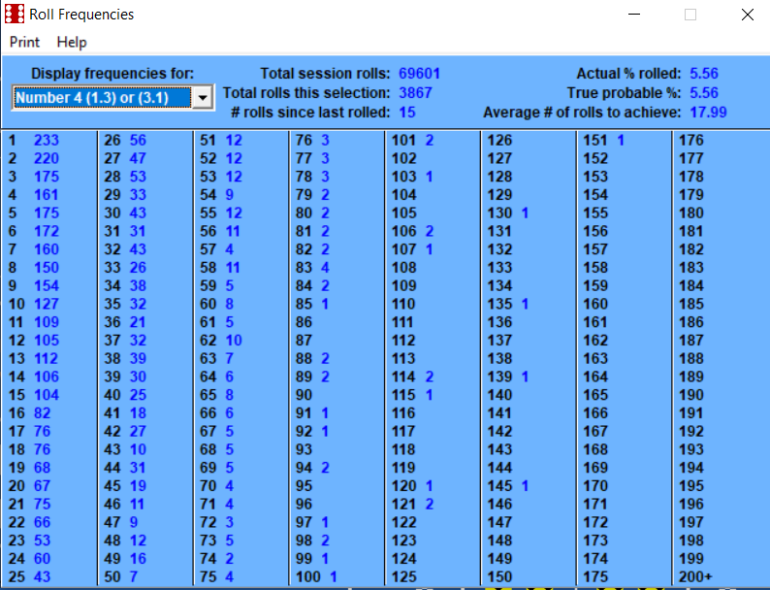
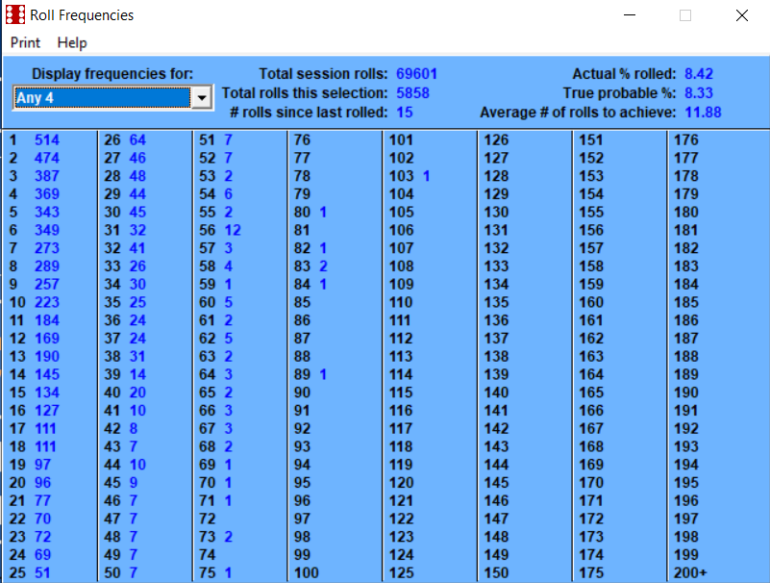
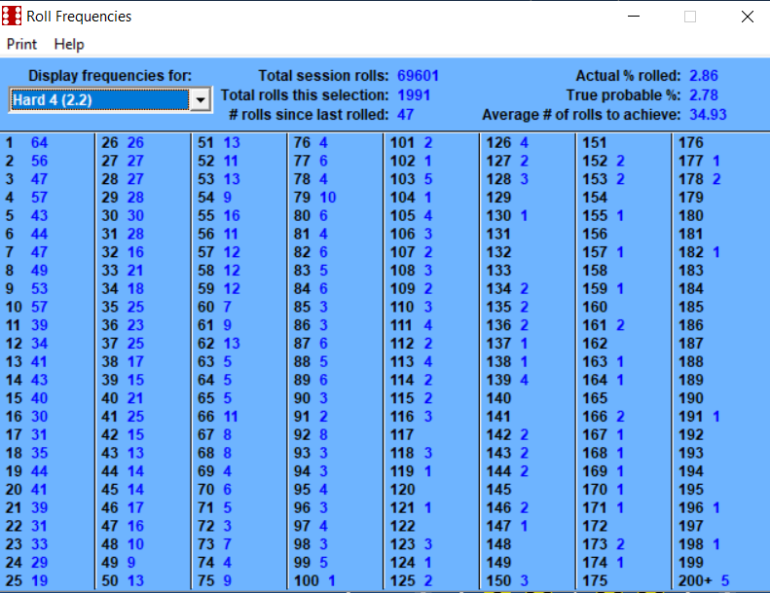
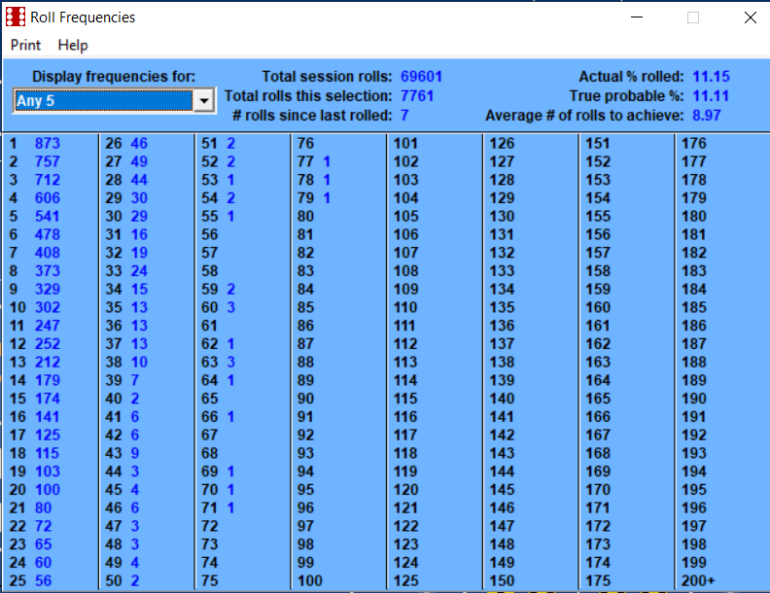
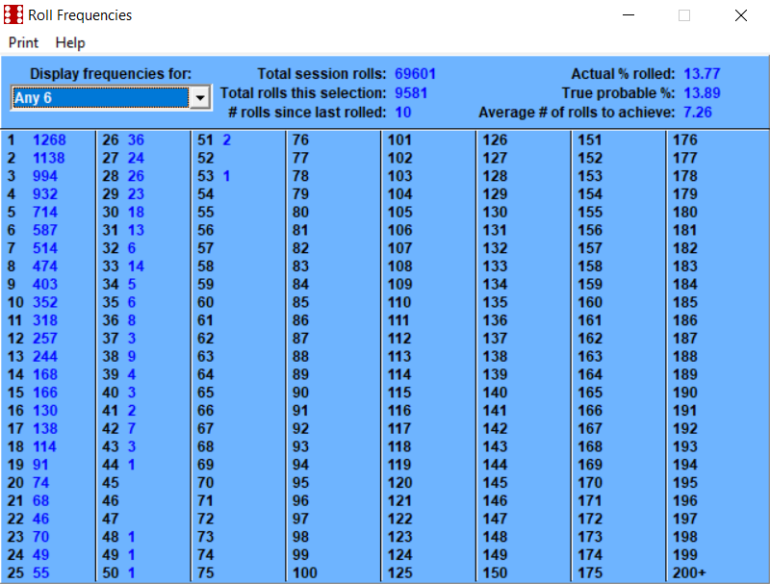
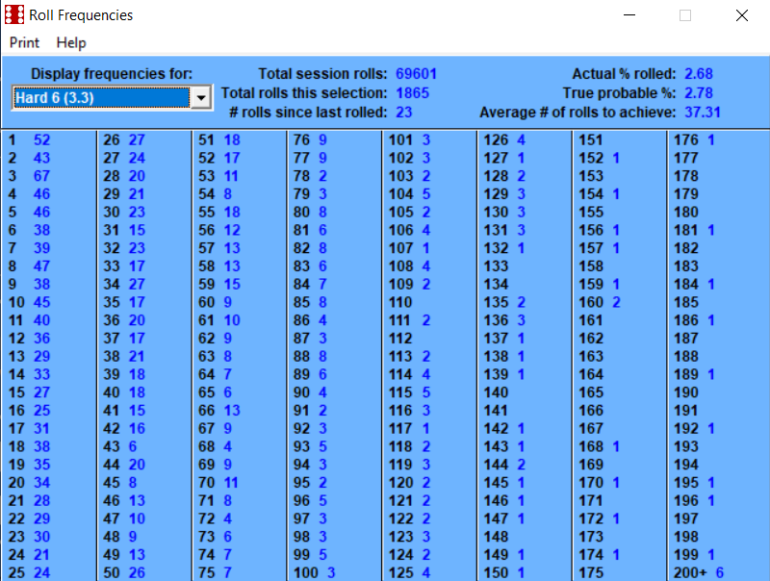
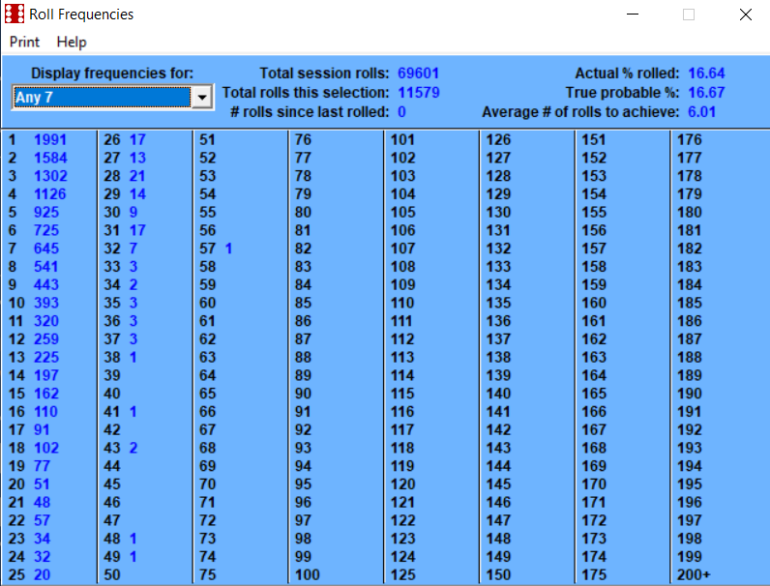
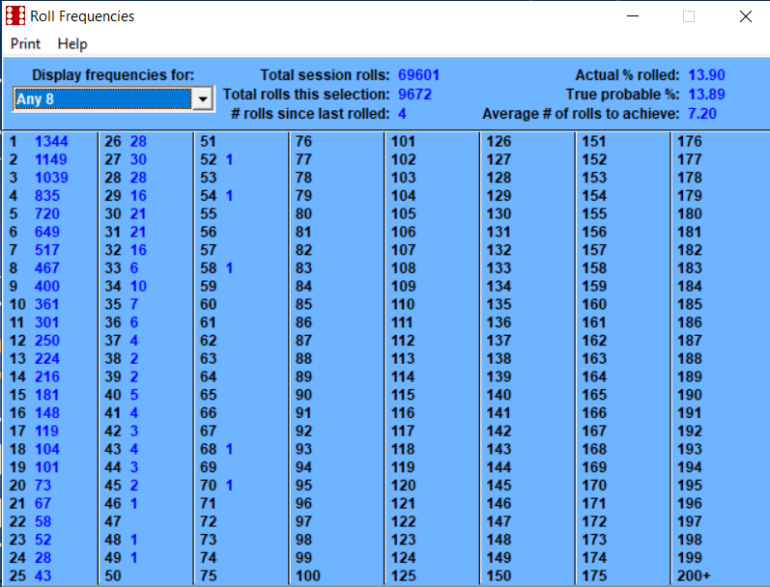
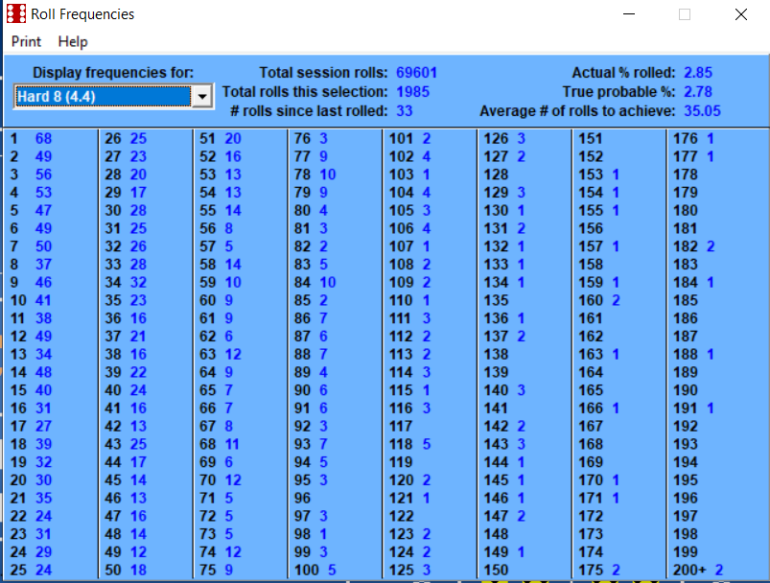
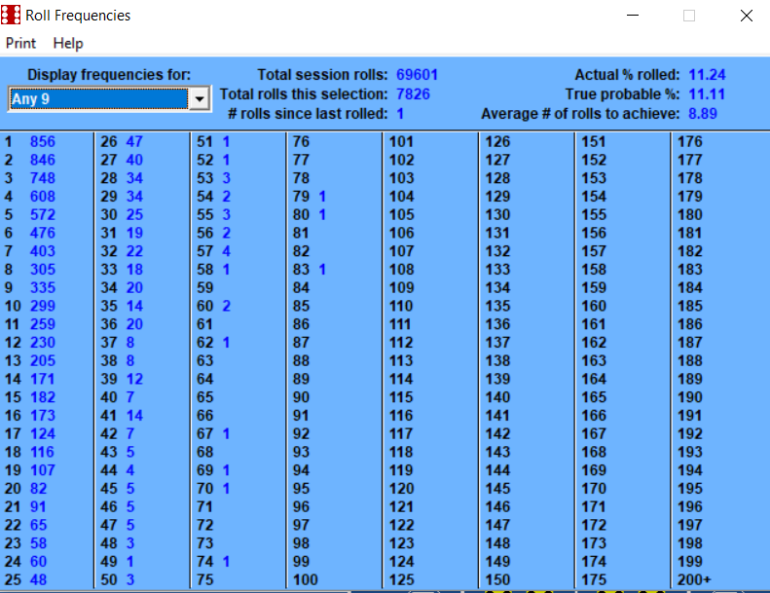
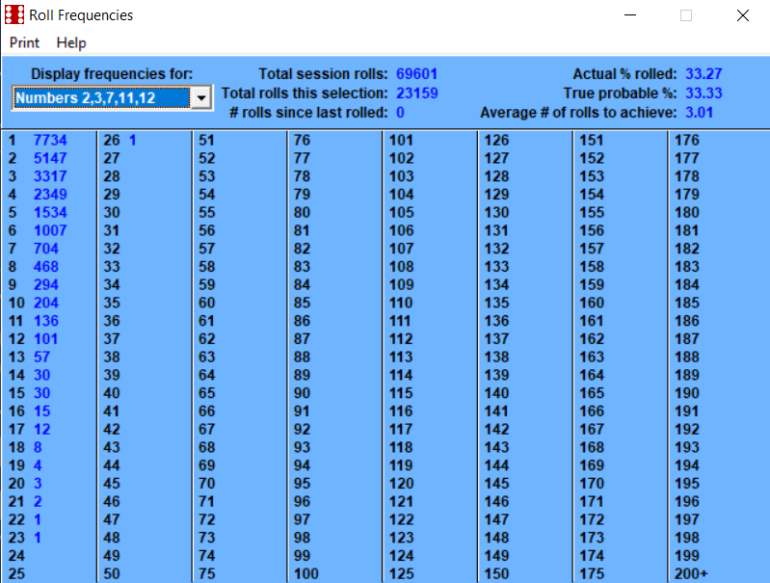
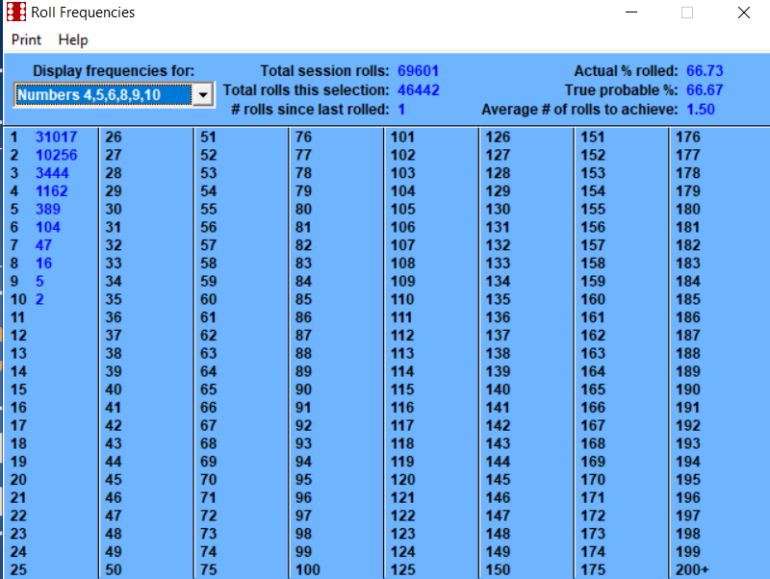
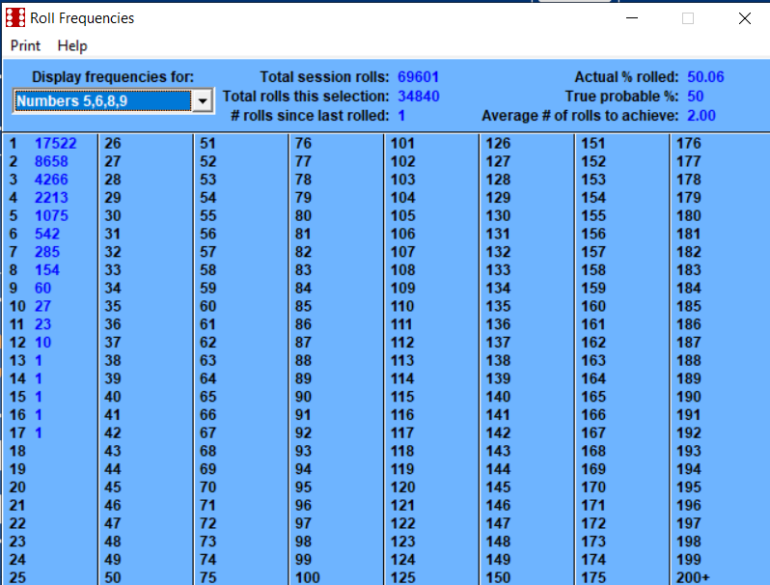
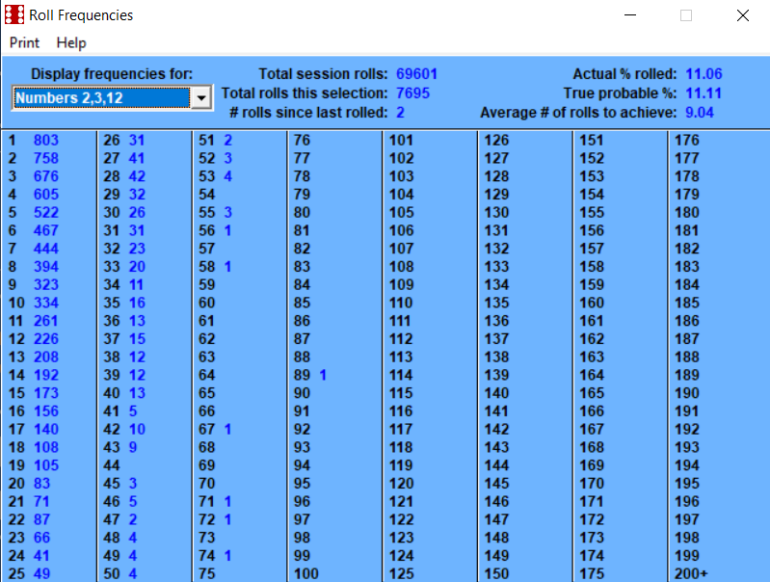
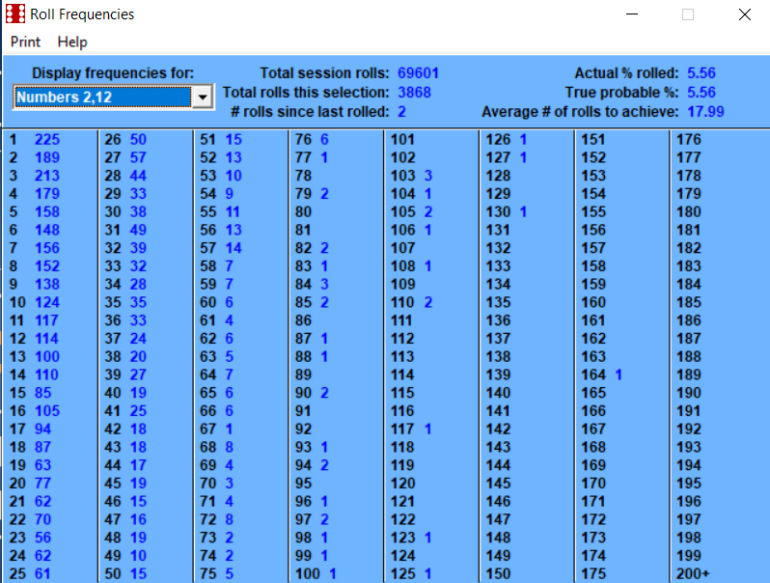
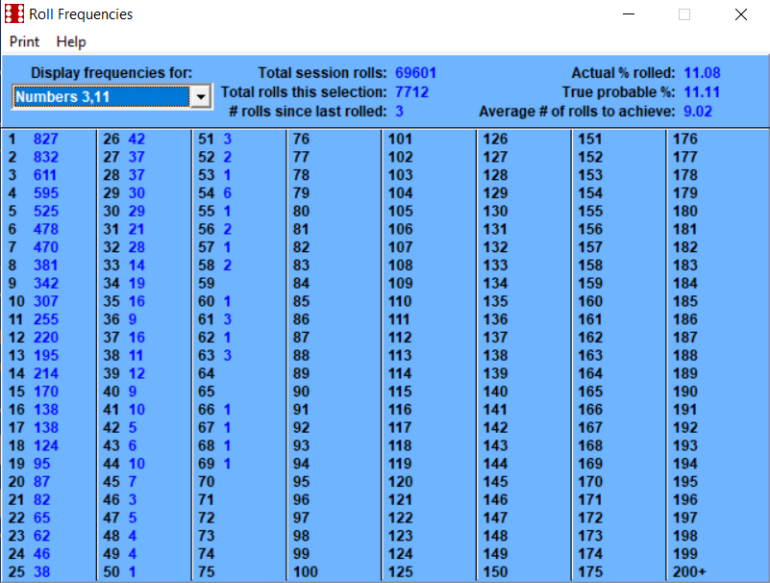
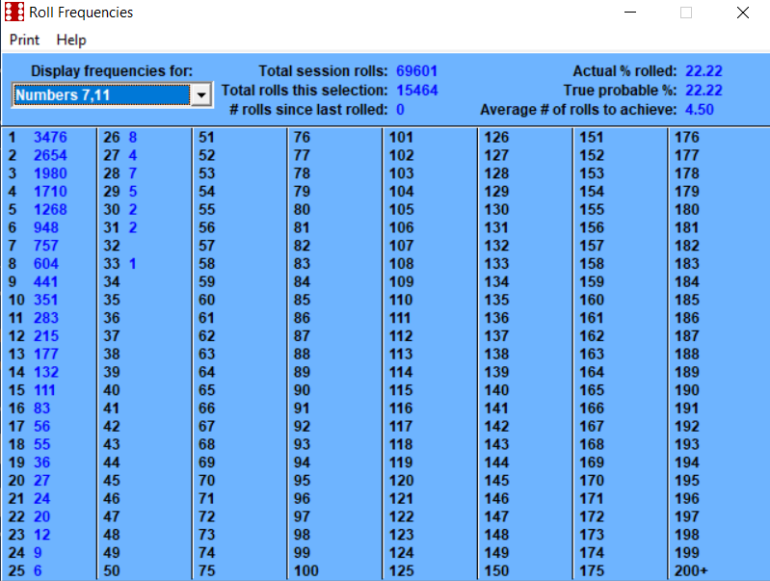
February 3rd, 2023 at 8:06:37 AM
permalink
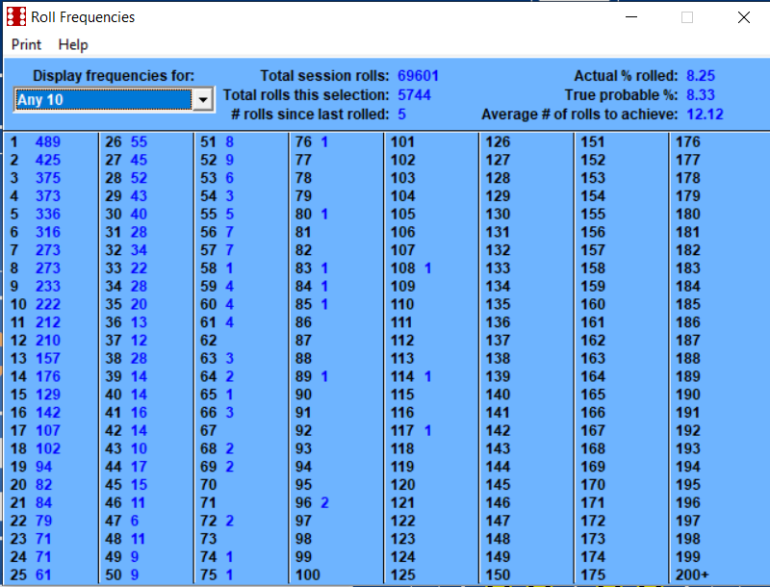
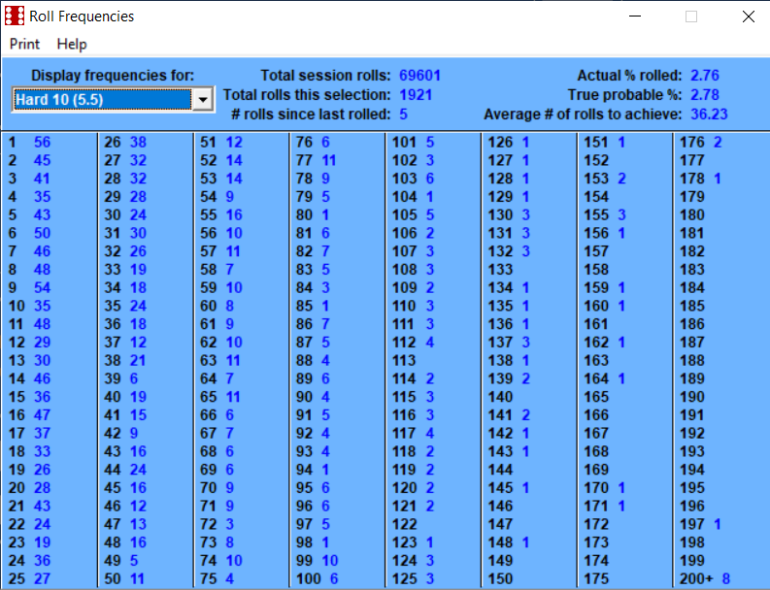
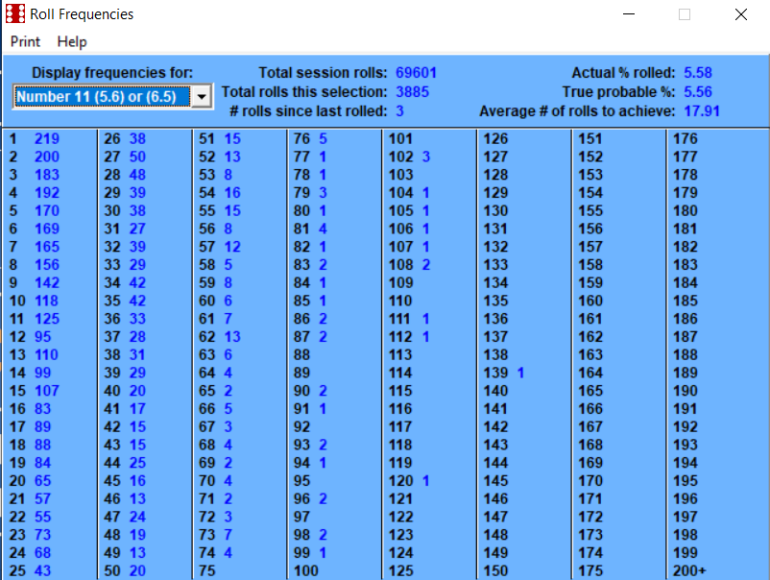
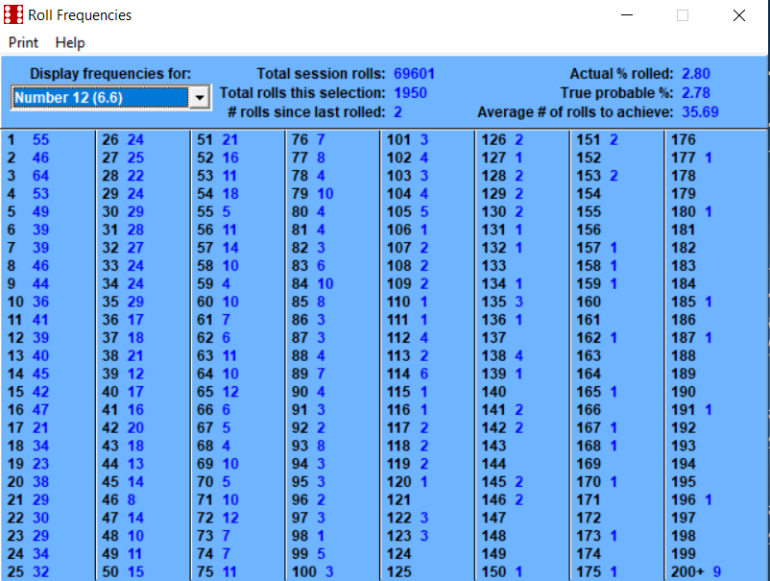
Betting the inside numbers of 5, 6, 8, 9 is a 50/50 probability.
This number of rolls is getting extremely close to the long term.
This number of rolls is getting extremely close to the long term.
February 3rd, 2023 at 8:46:52 AM
permalink
For those of us too math illiterate to know what's being said here... explain in a bit longer form way please?Quote: ChumpChangeBetting the inside numbers of 5, 6, 8, 9 is a 50/50 probability.
This number of rolls is getting extremely close to the long term.
link to original post
February 3rd, 2023 at 9:05:15 AM
permalink
Probability of 5 is (4/36)
Probability of 6 is (5/36)
Probability of 8 is (5/36)
Probability of 9 is (4/36)
Combined is (18/36)
Probability of 6 is (5/36)
Probability of 8 is (5/36)
Probability of 9 is (4/36)
Combined is (18/36)
"I suppose I was mad. Every great genius is mad upon the subject in which he is greatest. The unsuccessful madman is disgraced and called a lunatic." Fitz-James O'Brien, The Diamond Lens (1858)
February 3rd, 2023 at 9:46:56 AM
permalink
If you roll two dice (and add the total of the two dice) you can achieve various results ranging from 2, 3 ... 11, 12. As an example, because only 1-1 can produce a total of 2 there is only one way to roll 2. This is less likely to happen than a total of 3 which can be rolled two ways, either 1-2 or 2-1. You count two ways as the first die rolled could be 1 followed by the second being a 2, or the other way round. Similar logic applies for some of the other examples given, which are even more likely.Quote: ChallengedMilly...For those of us too math illiterate to know what's being said here... explain in a bit longer form way please?...
Using the "2" as an example, the second part is looking at how often you roll 2 (1-1). It is a similar problem to how often you might expect the Dealer to spin a specific Roulette Number (except there you have 37 or 38 slots, here we have 36). On average one might expect 1 in 36 of the rolls to be a winner. Similarly if one counts how long it takes before we have a winner, that also will be 36 rolls. The data presented confirms this is what happened.
If none of this makes sense then try this idea. Consider a very long road which has a mixture of houses and pubs (or cafes if you prefer!). In all the pubs you can have food and drink and also they have accomodation if needed. You are told that on this long road, on average one in six places are pubs, the rest are private houses. So you decide to go on a very long pub crawl! You reach the first pub, how long will it be before you reach the next one?
The chances of the next place being a pub is 1/6. If this doesn't happen the chances of the second place being a pub is (the first one wasn't) 5/6 * (the second one is) 1/6. This idea continues as it gradually becomes less likely you have a wait a long time to find a pub. However overall the average wait turns out to be 6 places.
Speaking of which - time to find a pub!!


