September 12th, 2014 at 2:14:31 AM
permalink
ok
I had some extra time on me hands
You can thank me any time.
in my opinion, Looks like you found the error(s) yourself and corrected them without admitting to it. It is a free country we live in.
Why, I do not know.
I make errors all the time in my code but I get them right in the end
in my opinion, I say it was the same errors you had from your online simulation program that you coded yourself, the one that used to be on your website.
The rail amounts after a decision comes to mind or what ever it was. It over-shot the win goal target
I can link to that thread if you so wish
I just know you removed that program and
I thought it was a good one, maybe the best one, that no one else had online, except for the simple to fix errors it produced.
==========================================
I did run 3 simulations this morning
1st was just 10k like mine and looks good as mine did two
2 others were 100k and looks good too
the photo just shows the first 2
I ran
see
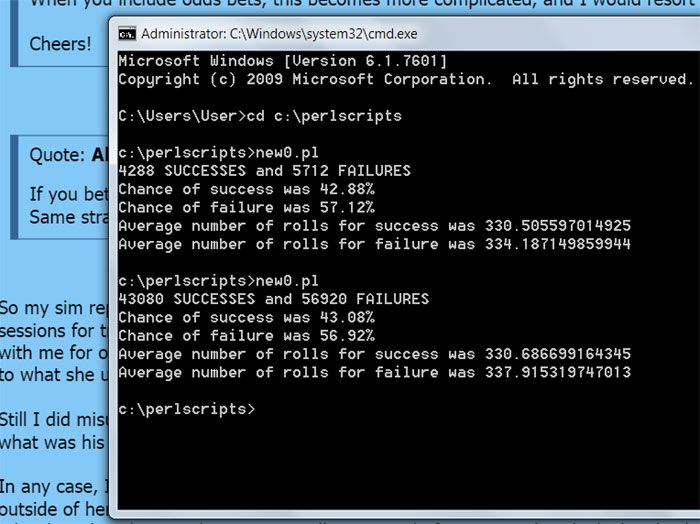
and see
the $1000 to $2000 by $10
yes I ran it all the way

my conclusion still
is your original code you used had error(s) that produced a very large error for the sample size you ran
you found them and fixed them, great job!
so here is the code I used, copied from your post and changed a few things to make changes easier
see if you can tell what I changed
I find no errors but maybe I added some without seeing them.
I also printed out a few sessions (your roll by roll) and that looked good too
Thank you Ahigh!
that was fun
Sally
I had some extra time on me hands
I finished the simulation for you.Quote: AhighSo my sim reports 40.349% compared to 42.98%.
That's close enough to indicate the sim is working and possibly I didn't run enough sessions for trials.
Run my simulation Sally.
You can find any problems yourself, if there are any. I'm not going to lead you by the hand to where the source code is. It's clearly posted in my first response of this thread.
You can thank me any time.
in my opinion, Looks like you found the error(s) yourself and corrected them without admitting to it. It is a free country we live in.
Why, I do not know.
I make errors all the time in my code but I get them right in the end
in my opinion, I say it was the same errors you had from your online simulation program that you coded yourself, the one that used to be on your website.
The rail amounts after a decision comes to mind or what ever it was. It over-shot the win goal target
I can link to that thread if you so wish
I just know you removed that program and
I thought it was a good one, maybe the best one, that no one else had online, except for the simple to fix errors it produced.
==========================================
I did run 3 simulations this morning
1st was just 10k like mine and looks good as mine did two
2 others were 100k and looks good too
the photo just shows the first 2
I ran
see

and see
the $1000 to $2000 by $10
yes I ran it all the way

my conclusion still
is your original code you used had error(s) that produced a very large error for the sample size you ran
you found them and fixed them, great job!
so here is the code I used, copied from your post and changed a few things to make changes easier
see if you can tell what I changed
I find no errors but maybe I added some without seeing them.
I also printed out a few sessions (your roll by roll) and that looked good too
#!/usr/bin/perl
$verbose = 0;
$initial_br = 100;
$min = 10;
$target = 200;
$sessions = 100000;
if( 0 )
{
$odds[4] = 3;
$odds[5] = 4;
$odds[6] = 5;
$odds[8] = 5;
$odds[9] = 4;
$odds[10] = 3;
}
else
{
$odds[4] = 0;
$odds[5] = 0;
$odds[6] = 0;
$odds[8] = 0;
$odds[9] = 0;
$odds[10] = 0;
}
sub roll
{
$rollcount++;
$d1 = int( rand( 6 ) + 1 );
$d2 = int( rand( 6 ) + 1 );
$sum = $d1 + $d2;
print "Roll was $d1-$d2 = $sum\n" if( $verbose );
}
sub resolve
{
if( $point == 0 )
{
if( $sum == 2 || $sum == 3 || $sum == 12 )
{
print "$sum craps $sum -- reel 'em in\n" if( $verbose );
$pass = 0;
}
elsif( $sum == 7 )
{
print "Seven winner seven pay the line\n" if( $verbose );
$br += $pass * 2;
$pass = 0;
}
elsif( $sum == 11 )
{
print "Yo eleven pay the line\n" if( $verbose );
$br += $pass * 2;
$pass = 0;
}
else
{
$point = $sum;
print "Point is $sum mark it up\n" if( $verbose );
}
}
elsif( $sum == $point )
{
print "$sum winner $sum pay the line\n" if( $verbose );
my( $save ) = $br;
$br += $odds + $pay[$sum] * $odds;
$br += $pass * 2;
$pass = 0;
$odds = 0;
print "Put \$" . ( $br - $save ) . " in rack ($br total) from hitting the $point\n" if( $verbose );
$point = 0;
}
elsif( $sum == 7 && $point > 0 )
{
print "Seven out!\n" if( $verbose );
$pass = 0;
$odds = 0;
$point = 0;
}
}
sub bet
{
if( $pass == 0 && $point == 0 && $br >= $min )
{
$br -= $min;
$pass = $min;
print "Betting $min on the pass with $br in the rail\n" if( $verbose );
}
elsif( $point > 0 && $odds == 0 )
{
my( $maxodds ) = $odds[$point] * $pass;
if( $br >= $maxodds )
{
$odds = $maxodds;
$br -= $odds;
}
elsif( $br >= $min )
{
$odds = $br;
$br = 0;
}
print "Betting \$$odds odds on the $point with $br in the rail\n" if( $verbose );
}
}
sub start_session
{
$br = $initial_br;
$pass = 0;
$odds = 0;
$rollcount = 0;
$point = 0;
}
sub totalbets
{
return $pass + $odds;
}
&start_session;
$pay[4] = 2;
$pay[5] = 3/2;
$pay[6] = 6/5;
$pay[8] = 6/5;
$pay[9] = 3/2;
$pay[10] = 2;
$point = 0;
&bet;
while( $success + $fail < $sessions )
{
&bet;
&roll;
&resolve;
if( $br >= $target )
{
print "+++ SUCCESS in $rollcount rolls\n\n" if( $verbose );
$success++;
$nrs += $rollcount;
&start_session;
}
elsif( $br < $min && &totalbets == 0 )
{
print "+++ FAILURE in $rollcount rolls\n\n" if( $verbose );
$fail++;
$nrf += $rollcount;
&start_session;
}
}
print "$success SUCCESSES and $fail FAILURES\n";
print "Chance of success was " . 100 * $success / ( $success + $fail ) . "%\n";
print "Chance of failure was " . 100 * $fail / ( $success + $fail ) . "%\n";
print "Average number of rolls for success was " . ( $nrs / $success ) . "\n";
print "Average number of rolls for failure was " . ( $nrf / $fail ) . "\n";
Thank you Ahigh!
that was fun
Sally
I Heart Vi Hart
September 12th, 2014 at 12:57:53 PM
permalink
Will someone tell me why you math geniuses can't round up or round down to the nearest full percentage? Is there something so mystical about to the nth decimal that makes it sensible to you? It's not sensible to me. Of course, I'm hardly a math genius. ; )
September 12th, 2014 at 1:03:12 PM
permalink
I explained this to you before, I think,Quote: Sonny44Will someone tell me why you math geniuses can't round up or round down to the nearest full percentage? Is there something so mystical about to the nth decimal that makes it sensible to you? It's not sensible to me. Of course, I'm hardly a math genius. ; )
on why I do what I do when I do
"Doooooooo"
a Paul McCartney quote
ask Ahigh, it is his perl code in the above photos.
I actually like them long...
Sally
I Heart Vi Hart


