How likely am I to get up by $100 by betting only pass line ($10) with no odds versus betting pass line ($10) with full odds.
How likely am I to double my money?
From my perspective, this is the most fundamental question to be asked about craps. Should I bet conservatively (no odds) in order to stretch out my bank roll or should I bet full odds and increase my variance, and possibly my winnings.
You are much more likely to double your $1000 by betting $10 with full odds than $10 flat with no odds.
You would be even more likely to get up $100 by playing a negative progression, starting at $100, flat with no odds, than to use odds.
You would be even more likely to get up $1000 by betting all $1000 one time on the line, than doing anything else.
Yeah, that would be great fun... but only if I happened to win.Quote: sodawaterYou would be even more likely to get up $1000 by betting all $1000 one time on the line, than doing anything else.
Quote: sodawaterYou are much more likely to get up $100 by betting $10 with full odds than $10 flat with no odds.
If you bet $10 flat trying to win $100 with no odds, you will double your money 40.349% of the time with an average of 377 rolls.
Same strategy will lose the $100 buy-in 59.651% of the time with an average number of 361 rolls.
If you bet $10 with 345x odds trying to win $100, you then have a 43.495% chance of success with an average of 21.22 rolls.
You have a 56.505% chance of failure with an average of 21.32 rolls.
So it appears from what I know that you are 7.779% more likely (43.496/40.349 - 1)*100% to win.
Betting odds shortens your session more than it improves your chances of winning when you bet 345x odds in my view, especially when NOT given explicit advice about how to use odds to have the best chance of doubling your money (like what you do when you don't have enough money for 345x odds, or betting slightly less to make it more likely to exactly meet your goal instead of haphazardly winning more because you always are betting 345x).
In the real world, on average a $100 buy-in at a $10 table will last you about four hours without playing odds and about 20 minutes when you play 345x. And this is just pass line with odds and no come bets by the way.
Quote: sodawaterYou are much more likely to double your $1000 by betting $10 with full odds than $10 flat with no odds.
You would be even more likely to get up $100 by playing a negative progression, starting at $100, flat with no odds, than to use odds.
You would be even more likely to get up $1000 by betting all $1000 one time on the line, than doing anything else.
When you get to 345x odds with $1000 bankroll, your chance of doubling your money actually improves compared to trying to double $100 with $10 and 345x odds. Similarly, flat-betting $10 trying to win $1000 is very nearly impossible. The house edge will overtake even the players with the highest endurance levels for boredom. You have about a 4.6% chance of making $1000 before losing $1000 with $10 on the pass line and no other bets. And it takes over 20,000 rolls on AVERAGE to do it, which is an AVERAGE of 200 playing hours or about five weeks at eight hours a day.
You have a 46.408% chance of winning. That's actually better than betting it all in the field (which has a 44% chance of at least doubling your money which includes a 2.78% chance of tripling your money and a 2.78% chance of quadrupling your money). The field is still a better approach than 345x if you want the biggest average win amount when you do win.
The average number of rolls to double your $1000 buy-in with $10 and 345x odds is 1449 rolls.
The average number of rolls to lose all $1000 with $10 and 345x odds is 1444 rolls.
At 100 rolls per hour, that's a 14-hour+ session.
The advantage play is ordering a $5 drink every fifteen minutes and tipping $1, which will net you $16/hour compared to the average loss of $4.00 per hour on the $10 passline @ 100 rolls per hour.
I simulated 100,000 sessions to come up with each of these calculations.
Just some sanity for those who actually believe things like "You are much more likely to get up $100 by betting $10 with full odds than $10 flat with no odds."
The generalization of this statement is true as the initial amount of money being wished to double increases. As the ratio of the flat bet on the passline decrease to the amount you wish to win, it becomes nearly impossible to double your money. But betting odds requires a bankroll. A bankroll that most people following this advice fail to understand with the other complexities going on related to the game.
Here's the truth: you're much more likely to have a quick and bad experience doing this believing that you have a significantly higher chance of accomplishing your goal because of the odds when in fact, you only have at most a 7.779% higher chance of accomplishing your goal and it will be at a eighteen times to the pace of play in terms of how long your buy-in lasts you.
#!/usr/bin/perl
$verbose = 0;
$initial_br = 1000;
$min = 10;
if( 1 )
{
$odds[4] = 3;
$odds[5] = 4;
$odds[6] = 5;
$odds[8] = 5;
$odds[9] = 4;
$odds[10] = 3;
}
else
{
$odds[4] = 0;
$odds[5] = 0;
$odds[6] = 0;
$odds[8] = 0;
$odds[9] = 0;
$odds[10] = 0;
}
sub roll
{
$rollcount++;
$d1 = int( rand( 6 ) + 1 );
$d2 = int( rand( 6 ) + 1 );
$sum = $d1 + $d2;
print "Roll was $d1-$d2 = $sum\n" if( $verbose );
}
sub resolve
{
if( $point == 0 )
{
if( $sum == 2 || $sum == 3 || $sum == 12 )
{
print "$sum craps $sum -- reel 'em in\n" if( $verbose );
$pass = 0;
}
elsif( $sum == 7 )
{
print "Seven winner seven pay the line\n" if( $verbose );
$br += $pass * 2;
$pass = 0;
}
elsif( $sum == 11 )
{
print "Yo eleven pay the line\n" if( $verbose );
$br += $pass * 2;
$pass = 0;
}
else
{
$point = $sum;
print "Point is $sum mark it up\n" if( $verbose );
}
}
elsif( $sum == $point )
{
print "$sum winner $sum pay the line\n" if( $verbose );
my( $save ) = $br;
$br += $odds + $pay[$sum] * $odds;
$br += $pass * 2;
$pass = 0;
$odds = 0;
print "Put \$" . ( $br - $save ) . " in rack ($br total) from hitting the $point\n" if( $verbose );
$point = 0;
}
elsif( $sum == 7 && $point > 0 )
{
print "Seven out!\n" if( $verbose );
$pass = 0;
$odds = 0;
$point = 0;
}
}
sub bet
{
if( $pass == 0 && $point == 0 && $br >= $min )
{
$br -= $min;
$pass = $min;
print "Betting $min on the pass with $br in the rail\n" if( $verbose );
}
elsif( $point > 0 && $odds == 0 )
{
my( $maxodds ) = $odds[$point] * $pass;
if( $br >= $maxodds )
{
$odds = $maxodds;
$br -= $odds;
}
elsif( $br >= $min )
{
$odds = $br;
$br = 0;
}
print "Betting \$$odds odds on the $point with $br in the rail\n" if( $verbose );
}
}
sub start_session
{
$br = $initial_br;
$pass = 0;
$odds = 0;
$rollcount = 0;
$point = 0;
}
sub totalbets
{
return $pass + $odds;
}
&start_session;
$pay[4] = 2;
$pay[5] = 3/2;
$pay[6] = 6/5;
$pay[8] = 6/5;
$pay[9] = 3/2;
$pay[10] = 2;
$point = 0;
&bet;
while( $success + $fail < 100000 )
{
&bet;
&roll;
&resolve;
if( $br >= $initial_br * 2 )
{
print "+++ SUCCESS in $rollcount rolls\n\n" if( $verbose );
$success++;
$nrs += $rollcount;
&start_session;
}
elsif( $br < $min && &totalbets == 0 )
{
print "+++ FAILURE in $rollcount rolls\n\n" if( $verbose );
$fail++;
$nrf += $rollcount;
&start_session;
}
}
print "$success SUCCESSES and $fail FAILURES\n";
print "Chance of success was " . 100 * $success / ( $success + $fail ) . "%\n";
print "Chance of failure was " . 100 * $fail / ( $success + $fail ) . "%\n";
print "Average number of rolls for success was " . ( $nrs / $success ) . "\n";
print "Average number of rolls for failure was " . ( $nrf / $fail ) . "\n";
Quote: geoffIf your goal is to increase your bankroll then you should always take full odds. The odds have a house edge of 0 while you passline has a HE of 1.41%. If your goal is to play for as long as possible then bet no odds.
If your goal is to increase your bankroll, you should either work more and gamble less, or learn how to advantage play. IN THE LONG RUN increasing your odds does not improve your chance of increasing your bankroll more than it increases your chance of reducing your bankroll. So I would suggest that your statement is incorrect.
IN THE SHORT RUN you only make your point 40% of the time. The remaining 60% of the time you will lose your odds bet on average. So in the SHORT run, if your goal is increasing your bankroll, you want to lay odds, not take them as you're more likely to win that way.
The funny thing about dice is that they don't care what you are trying to do. And in the LONG RUN the most practical thing that odds do for a player is to temporarily give them money in the rail that is an opportunity for a dealer to beg for a tip. That's a house edge too, you know. Or maybe you could call it a "dealer edge." There is a reason dealers remind you about betting more odds.
Quote: AhighIf your goal is to increase your bankroll, you should either work more and gamble less, or learn how to advantage play. IN THE LONG RUN increasing your odds does not improve your chance of increasing your bankroll more than it increases your chance of reducing your bankroll. So I would suggest that your statement is incorrect.
IN THE SHORT RUN you only make your point 40% of the time. The remaining 60% of the time you will lose your odds bet on average. So in the SHORT run, if your goal is increasing your bankroll, you want to lay odds, not take them as you're more likely to win that way.
The funny thing about dice is that they don't care what you are trying to do. And in the LONG RUN the most practical thing that odds do for a player is to temporarily give them money in the rail that is an opportunity for a dealer to beg for a tip. That's a house edge too, you know. Or maybe you could call it a "dealer edge." There is a reason dealers remind you about betting more odds.
This has got to be your most acutely poignant post that I've read.
Bankroll $1000 and $10 flat bets (bankroll units = 100. So it does not now matter what your $ unit is. bankroll of $100 and flat bet of $1 is equal to a Bankroll of $2500 and $25 flat bets and on and on)
and this post will finally set me as my syndicates' official number cruncher.
Super!
I mean I do have the legs for it, as I am also told.
Nice questions I see.Quote: longtimelancerSay I have a bankroll of $1000 and I would like to try to make $100. $10 table with 3-4-5X odds.
How likely am I to get up by $100 by betting only pass line ($10) with no odds versus betting pass line ($10) with full odds.
How likely am I to double my money?
many ask these type of questions all the time
Ahigh's post above looks to have many results that differ from mine.
We both can not be 100% correct here.
Ahigh has a past history of posting result errors, why? Don't know and don't care.
I have a past and current history of copy/paste problems (wrong data copied) I say because of my fat fingers
But not all care to be gifted IMO.
I do like to dot my eyes and cross my tees.
How much more likely?Quote: sodawaterYou are much more likely to get up $100 by betting $10 with full odds than $10 flat with no odds.
goal: $100 win (10 units) or BUST trying (for simulations, bust also includes the sessions where a full bet is not able to be made)
Using the Gambler's Ruin formula that has been around and derived by many over the last 350 years
no odds
success = 74.2149768% with an average number of trials = 1,298.56
simulation by 1 million shooters
Avg. No. games played . = 1295.79
Avg. No. dice rolls . . = 4374.35
Bankroll was busted . . = 25.741% of the time ( 257414)
Win goal was met . . . = 74.259% of the time ( 742586)
added:
as pointed out, it can take a lot of time to hit your win goal.
74.2149768% is really a limit
here are some probabilities and trials
200: 0.41382205
500: 0.560445529
1000: 0.638792258 ruin: 0.005341015
2000: 0.692413962 ruin: 0.063885309
Now using the odds at 345x
Using a transition matrix
(matrix algebra. I was not exposed to this in High School, but in college for 2 weeks meaning I really had to learn this on my own. Actually, everyone should be taught this by High School IMO. Most use it but are not aware that they do)
345x odds = 88.406245%
(at first I had only 80% but I noticed I had the win goal set for $200 or 20 units. My first error found)
simulation by 1 million shooters
Avg. No. games played . = 53.23
Avg. No. dice rolls . . = 179.74
Bankroll was busted . . = 11.725% of the time ( 117248)
Win goal was met . . . = 88.275% of the time ( 882752)
summary
$1000 into $1100
ONE attempt probability
88.406245% with 345X odds
74.2149768% with 0 odds
and do not forget this
"You are much more likely to get up $100 by betting..."
I see a difference
SureQuote: sodawaterYou are much more likely to double your $1000 by betting $10 with full odds than $10 flat with no odds.
goal: to DOUBLE the starting bankroll or bust out trying.
This assumes that the player does not remove money from the Bankroll if it increases during play.
That would result in a different question and result
success = 5.5804887% with an average number of trials = 6,282.19
=1/((q/p)^b_x+1) where b_x = bankroll units
simulation by 1 million shooters
Avg. No. games played . = 6278.16
Avg. No. dice rolls . . = 21193.64
Bankroll was busted . . = 94.397% of the time ( 943966)
Win goal was met . . . = 5.603% of the time ( 56034)
transition matrix
345x odds = 46.885%
simulation by 1 million shooters
Avg. No. games played . = 425.40
Avg. No. dice rolls . . = 1436.06
Bankroll was busted . . = 53.498% of the time ( 534979)
Win goal was met . . . = 46.502% of the time ( 465021)
summary
$1000 into $2000 (100 units into 200 units)
ONE attempt probability
46.885% with 345X odds
5.5804887% with 0 odds
How about Bold Play here.Quote: sodawaterYou would be even more likely to get up $100 by playing a negative progression, starting at $100, flat with no odds, than to use odds.
Bet $100, lose bet $200, lose bet $400
sounds like a Marty!
But a loss here means next bet is all-in for $300.
I set this up in Excel and BruceZ was kind enough to set the code up for the free program R
success = 0.904106868
only 0.901300869 by and including the 5th bet
my Excel
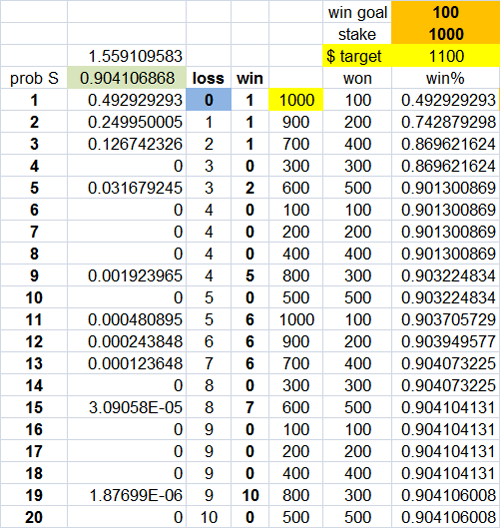
in R
[1] 0.9041068
R code
pdoub = function(br,goal,max_bet,pwin,odds,thresh,prob=1) {
if (br < 1 | prob < thresh) return(0)
bet = ceiling((goal-br)/odds) # bet needed to reach goal
limit = min(br,max_bet) # limit = max bet possible
if ( bet < limit )
pwin + (1-pwin)*pdoubb(br-bet,goal,max_bet,pwin,odds,thresh,prob*(1-pwin))
else
pwin*pdoubb(br+odds*limit,goal,max_bet,pwin,odds,thresh,prob*pwin) + (1-pwin)*pdoubb(br-limit,goal,max_bet,pwin,odds,thresh,prob*(1-pwin))
}
require(compiler)
pdoubb = cmpfun(pdoub)
system.time(p <- pdoubb(1000,1100,5000,244/495,1,0.0000001))
pyes, but many would find this type of play not fun at all.Quote: sodawaterYou would be even more likely to get up $1000 by betting all $1000 one time on the line, than doing anything else.
Less than 2 bets on average for success and failure
Maybe also also because you can lose more times, on average, than you win.
> pdoub = function(br,goal,max_bet,pwin,odds,thresh,prob=1) {
+ if (br < 1 | prob < thresh) return(0)
+ bet = ceiling((goal-br)/odds) # bet needed to reach goal
+ limit = min(br,max_bet) # limit = max bet possible
+ if ( bet < limit )
+ pwin + (1-pwin)*pdoubb(br-bet,goal,max_bet,pwin,odds,thresh,prob*(1-pwin))
+ else
+ pwin*pdoubb(br+odds*limit,goal,max_bet,pwin,odds,thresh,prob*pwin) + (1-pwin)*pdoubb(br-limit,goal,max_bet,pwin,odds,thresh,prob*(1-pwin))
+ }
> require(compiler)
> pdoubb = cmpfun(pdoub)
> system.time(p <- pdoubb(1000,2000,5000,244/495,1,0.0000001))
user system elapsed
0.00 0.00 0.06
> p
[1] 0.4929292
final summary (100 units into 110 units)
$1000 into $1100
90.410687% from Bold Play
88.406245% with 345X odds
74.2149768% with 0 odds
$1000 into $2000 (100 units into 200 units)
49.2929% from Bold Play
46.885% with 345X odds
5.5804887% with 0 odds
Sally Oh
FalseQuote: AhighSo in the SHORT run, if your goal is increasing your bankroll, you want to lay odds, not take them as you're more likely to win that way.
First define the short run in terms of how many bets are going to be made, the size of those bets and the starting bankroll and the target bankroll to be used.
this sets the playing field so no one has an advantage.
This should be so much fun!
Then
show your proof for "you're more likely to win that way"
not like
How a pass line bet magically turns into a put bet when the point is established.
funny funny stuff now
Oh, do not forget to address variance because it dominates the short run
and see you after Wednesday
off to the casinos in SoCal
Sally Oh
Quote: mustangsallyFalseQuote: AhighSo in the SHORT run, if your goal is increasing your bankroll, you want to lay odds, not take them as you're more likely to win that way.
First define the short run in terms of how many bets are going to be made, the size of those bets and the starting bankroll to be used.
this sets the playing field so no one has an advantage.
This should be so much fun!
Then
show your proof for "you're more likely to win that way"
not like
How a pass line bet magically turns into a put bet when the point is established.
funny funny stuff now
Oh, do not forget to address variance because it dominates the short run
and see you after Wednesday
off to the casinos in SoCal
Sally Oh
I know how it pains you to admit that you are wrong.
An average odds bet wins 1/3rd of the time for a four or a ten, 2/5ths of the time for a five or nine, and 5/11ths of the time for a six or an eight.
I know that you know this.
The chance of establishing a four or ten is 6/24, a five or nine is 8/24, and six or eight is 10/24.
So
6/24ths of points have 1/3 chance of winning
8/24ths of points have 2/5 chance of winning
10/24ths of points have 5/11 chance of winning
(6/24)*(1/3) + (8/24)*(2/5) + (10/24)*(5/11) = 40.60606060606 chance of winning a free odds bet.
Given that there is no house edge, it's easy to know that 100-40.606060 is the chance of winning an average lay odds bets. So that's 59.393939%
My assertion is that if you want to make a single free bet, you are more likely to win the lay odds bet.
The shortest run is a single bet. In the long run (millions of samples that I doubt you have in your play) neither one is better than another.
But there are more folks making a single bet and leaving than folks making a million bets.
If your argument is that a single bet is not a short run, please elaborate. But I am 100% certain that I am right in the short run of a single bet.
Transitively, your assertion that my statement is false is as wrong as other false assertions that you have made about my claims.
I know it hurts to be wrong when you work so hard on your answers. And maybe you can point out an example where you admitted that I was right and you were wrong. The Wizard just did that two days ago, but I can't recall a single instance of you doing that for me.
Here's what I think. I think you feel that you are smarter than I am and it burns you up to have to admit that someone who you consider to be less intelligent that you is correct about something that you disagree with.
So go ahead and tell me how that a single bet is not a short run approach. In fact, if you're really more math orientated than an actual player who actually plays the game, maybe you can calculate the chance of winning on average for a sequence of max odds versus max lay odds bets where n is a small number between 1 and 100. I have already proven that when n is one, you're going to win 60% of the time versus 40% of the time. Given that all sample sizes include at least one bet, I think that until the sample size is greater than one, you have no chance of having a better chance of winning among those who consider "short runs" to include a single bet. Maybe you could define "run" as requiring at least two samples to support your theory that laying odds doesn't increase your chance to win up to 60%!
I personally think you come up with theoretical answers that often don't have any application to the average real-world craps gambler, and that your writing reflect a less pragmatic and more pedagogical (and therefore less practical) approach to the game.
You seem very out of touch with the masses who enjoy the game.
I could be wrong.
There's a statement I have never seen you post.
Quote: treetopbuddyI wonder what the view is like from the Ivory Towers.
He can see the strip from there.
read what you wroteQuote: Ahighin the SHORT run, if your goal is increasing your bankroll, you want to lay odds, not take them as you're more likely to win that way.
"if your goal is increasing your bankroll"
YES
IT IS FOR ALL CRAPS PLAYERS
"you want to lay odds, not take them as you're more likely to win that way."
sure you are more likley to win laying the odds bet one time
what is FALSE is
"if your goal is increasing your bankroll, you want to lay odds, not take them as you're more likely to win that way."
FALSE
show your proof and state the parameters
this will be fun
Sally
added: The OP may be interested in don't pass with lay odds instead of pass line with odds to hit win targets
The difference is not going to be much
but we will see how much
Quote: mustangsallyone more time
read what you wrote
"if your goal is increasing your bankroll"
YES
IT IS FOR ALL CRAPS PLAYERS
"you want to lay odds, not take them as you're more likely to win that way."
sure you are more likley to win laying the odds bet one time
what is FALSE is
"if your goal is increasing your bankroll, you want to lay odds, not take them as you're more likely to win that way."
FALSE
show your proof and state the parameters
this will be fun
Sally
added: The OP may be interested in don't pass with lay odds instead of pass line with odds to hit win targets
The difference is not going to be much
but we will see how much
Look what YOU wrote. You write some of the most obviously false overly broad blanket statements I have seen, even including samples from very unintelligent posters.
If you honestly think that increasing your bankroll is the goal for all craps players, you need some professional help.
They make brochures called, "when the fun stops."
And it's not fun. Your posts are inflammatory rather than entertaining for me. Your posting style is self-righteous and difficult to understand for some. Trust and know that I have absolutely no interest in participating in what you think would be fun for you. That comment sounds simply sadistic, frankly.
Who needs math when they cheat ?Quote: treetopbuddyI'm guessing Archie Karas didn't stop to consider the math when he took Binons for 30 million plus.......
Quote: AxelWolfWho needs math when they cheat ?
Are you saying Kara's was cheating during "the run" in the early 90's?
Quote: treetopbuddyAre you saying Kara's was cheating during "the run" in the early 90's?
I never met or knew much about Archie. But when I found out he was a cheater, it definitely added significant doubt that he did not cheat during his world-famous run.
I have not heard of any evidence that he cheated for this run. But I do expect he was doing anything and everything that he could legally do in order to attempt to get an advantage.
I also expect his losses were a result of human emotion and denial of the risks he was undertaking to lose that money.
On a smaller scale, many people have found themselves ahead more than they expected, and as a result, divorced themselves from the very risk of losing real money that, in their mind, was more easily obtained (the circumstances of winning) than reality would dictate for the future.
When I hear people talking about "the house's money" -- that's a tell-tale sign that someone does not appreciate the risks of subsequent moves in taking further risks.
Money is money is money is money in mind. Free play, coupon, bitcoin, gold, real property. Value is value no matter how lucky you were to come into possession, it does not change the value of the money.
Getting a false sense of security that you will always have money because of the ease in which you obtained money in the past is a very dangerous thing!
Live and learn is how most people understand this, unfortunately. That certainly includes me.
In order to make any odds wager on the line the point must have already been established.
You will never win or lose an odds wager on a pass/don't bet on a come out roll.
You are decidedly more likely to win a DP odds wager than a Pass odds wager - but the payoff works the opposite direction making both wagers effectively equal. Hence the whole "no house edge" thing on odds bets.
DP has a very slight edge overall but the odds play out the same way on both sides.
I wasn't there, I don't know him personally and i'm not judging, but from what i have heard, yes.Quote: treetopbuddyAre you saying Kara's was cheating during "the run" in the early 90's?
Using him as a testament to "Math? we don't need no stinking math." is probably not a good choice
Quote: mustangsally
final summary (100 units into 110 units)
$1000 into $1100
90.410687% from Bold Play
88.406245% with 345X odds
74.2149768% with 0 odds
$1000 into $2000 (100 units into 200 units)
49.2929% from Bold Play
46.885% with 345X odds
5.5804887% with 0 odds
Sally Oh
Thank you so much! This is great information.
Another question: What is the chance of never being "up" betting 0 odds and betting 345X odds? For both pass and don't pass. Assuming infinite bankroll.
Could you also include a simulation based on betting both continuous Come and Don't Come for the 100 units to 110 units? I assume that wouldn't change the percentages, just the number of rolls to get there.
Also, it would be fascinating to see the statistical distribution of these simulations rather than just the edge (mean) and the SD. The skewness and the kurtosis are also important parameters in deciding how and what to play. For instance, video poker has a great edge and a large SD but the distribution must be highly skewed thanks to so much of the return coming from the royal and straight flushes. To have all of the distributions from BJ, Craps (0 odds and 345X), Roulette, PaiGow Poker, Baccarat, Video Poker, etc. ON THE SAME GRAPH would be Very Valuable.
I misunderstood the original question. I thought you were trying to turn $100 into $200 not $1000 into $1100.
That might explain the different answers I received.
It's not often that I see anyone trying to win $100 risking $1000. But it seems a high percentage of players I observe are trying to double a $100 buy-in.
Even still, I got 4.6% compared to Sally's 5.58% with zero odds attempting to turn $1000 into $2000.
And I got 46.408% compared to Sally's 46.885% doing the same thing with 345x.
Quote: AxelWolfI wasn't there, I don't know him personally and i'm not judging, but from what i have heard, yes.
Using him as a testament to "Math? we don't need no stinking math." is probably not a good choice
Luck and balls trump stinking math.......at least some of the time.
0%.Quote: longtimelancerAnother question: What is the chance of never being "up" betting 0 odds and betting 345X odds? For both pass and don't pass. Assuming infinite bankroll.
If you have an infinite bankroll, and infinite time, you are guaranteed to get to the good at some point. Awesomely, you are even guaranteed to do it infinite times. [I could be wrong on these results, my Infinite Markov Chains might be rusty]
However, for any finite bankroll (say the current US money supply) there exists a positive chance that you will not make it above water. My point is mathematically these results is valid, however it has no bearing on reality. What is much more useful would be the results for bankrolls of 1k, 10k, and 100k trying to just get "up."
Also for these kinds of goals one should consider negative progressions instead of waiting the random walk (flat betting) to break your way.
Edit: added useful link for anyone interested in MCs http://www.math.uchicago.edu/~may/VIGRE/VIGRE2011/REUPapers/Johnston.pdf
Quote: mustangsally
summary
$1000 into $1100
ONE attempt probability
88.406245% with 345X odds
74.2149768% with 0 odds
and do not forget this
"You are much more likely to get up $100 by betting..."
I see a difference
Are you trying to say that an 88.4% chance of success is not "much more likely" than a 74.2% chance? In the context of choosing between two betting options, I would certainly consider a 14 percentage point difference enough to call it "much better." We call blackjack a much better bet than roulette and that's only a 4 percentage point difference, not 14.
I would guess this might slightly improve your chances. I would say this because now the results of your bets will be correlated with each other, thereby giving you effectively a larger bet size. I am also assuming the continuous system stops placing additional bets once there is sufficient action on the table to make it above 110 given the resolution of those bets.Quote: longtimelancerCould you also include a simulation based on betting both continuous Come and Don't Come for the 100 units to 110 units? I assume that wouldn't change the percentages, just the number of rolls to get there.
Quote: endermike0%.
If you have an infinite bankroll, and infinite time, you are guaranteed to get to the good at some point. Awesomely, you are even guaranteed to do it infinite times. [I could be wrong on these results, my Infinite Markov Chains might be rusty]
However, for any finite bankroll (say the current US money supply) there exists a positive chance that you will not make it above water. My point is mathematically these results is valid, however it has no bearing on reality. What is much more useful would be the results for bankrolls of 1k, 10k, and 100k trying to just get "up."
Also for these kinds of goals one should consider negative progressions instead of waiting the random walk (flat betting) to break your way.
Edit: added useful link for anyone interested in MCs http://www.math.uchicago.edu/~may/VIGRE/VIGRE2011/REUPapers/Johnston.pdf
Yes, You are right of course. The 1K, 10K, 100K question is much more relevant. Or maybe 100, 1000 and 10,000 unit bankroll.
Quote: Ahighlongtimelancer,
I misunderstood the original question. I thought you were trying to turn $100 into $200 not $1000 into $1100.
That might explain the different answers I received.
It's not often that I see anyone trying to win $100 risking $1000. But it seems a high percentage of players I observe are trying to double a $100 buy-in.
Even still, I got 4.6% compared to Sally's 5.58% with zero odds attempting to turn $1000 into $2000.
And I got 46.408% compared to Sally's 46.885% doing the same thing with 345x.
No problem. Thanks for taking the time to answer it. It is always good to get multiple opinions.
it sure is as long as the values (opinions) are close.Quote: longtimelancerNo problem. Thanks for taking the time to answer it. It is always good to get multiple opinions.
how about if they are not?
would you then rather have a correct answer or just an opinion.
My answers were from simulations and direct calculations that any one can duplicate.
That way I can double check myself. and I find myself making so many mistakes this way that are easy to correct.
Ahigh posted (or left after he deleted much of his post about me. coolness)
"Even still, I got 4.6% compared to Sally's 5.58% with zero odds attempting to turn $1000 into $2000.
And I got 46.408% compared to Sally's 46.885% doing the same thing with 345x."
I even saw how he rambled on about how accurate my answers (opinion) could be, but I see he deleted that part
Oh,
Both of us showed results that are close.
our second values are real close but not the first one.
especially considering that 5.58% can be calculated two different ways, no sim needed.
Why is Ahigh's answer so far off?
I would have thought 5.6% would have been his answer but now we have to wait and see why.
does it matter if it is 4.6% or 5.58%? Not really if one thinks the true answer is closer to 65%
all for fun while learning
maybe it is time to show the steps to calculate this example.
the Gambler's Ruin formula is easy to find.
do have fun!
Sally
hope you have as much fun playing craps as you do posting questions about it
Quote: sodawater
You would be even more likely to get up $1000 by betting all $1000 one time on the line, than doing anything else.
This, it turns out is not true. See "Improving at Bold Play in Craps" by Ethier.
Basically Ethier showed that the (nearly?) optimal (in the sense of reaching a certain goal) is to bet the odds boldy, that is arrange it so that you are betting the maximum amount of odds consistent with not overshooting your goal and the rules of the casino.
Quote: DrEntropyThis, it turns out is not true. See "Improving at Bold Play in Craps" by Ethier.
Basically Ethier showed that the (nearly?) optimal (in the sense of reaching a certain goal) is to bet the odds boldy, that is arrange it so that you are betting the maximum amount of odds consistent with not overshooting your goal and the rules of the casino.
Yeah, craps kind of throws a wrench into the "bold play" strategy because you don't know a priori how much you will be able to bet!
https://wizardofodds.com/games/craps/#toc-Strategy
Quote: TerribleTomThe house edge table over at WoV seems to indicate that the higher the odds wager the lower the house edge.
https://wizardofodds.com/games/craps/#toc-Strategy
Because for some reason, the Wizard and others think by placing a 0 edge bet it reduces your overall disadvantage & they calculate the edge of the flat bet and the odds together. Ridiculous.
May as well calculate BJ the same way (average $ in action vs average loss).
*might explain*Quote: Ahighlongtimelancer,
I misunderstood the original question. I thought you were trying to turn $100 into $200 not $1000 into $1100.
That might explain the different answers I received.
what needs explaining is how you got your results for what follows next
as they appear to be way out in left field.
True or False?Quote: AhighIf you bet $10 flat trying to win $100 with no odds, you will double your money 40.349% of the time with an average of 377 rolls.
Same strategy will lose the $100 buy-in 59.651% of the time with an average number of 361 rolls.
I say False.
what code or calculations produced your results?
for me
two simple formulas return
"to double a $100 bankroll with $10 flat bets (10 unit bankroll)"
42.97559%
I use excel to calculate this for me
see
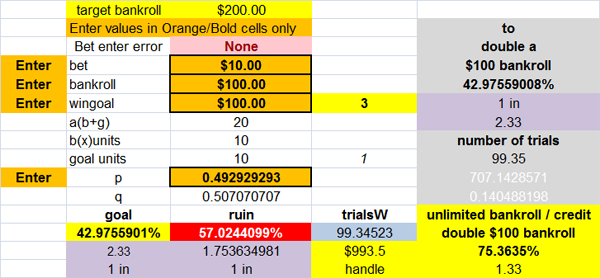
Ahigh's error = 0.0262659 / 40.349% = 6.51%
a typo?
"explain the different answers I received"
a fast sim of 1 million players
Avg. No. games played . = 99.38
Avg. No. dice rolls . . = 335.50
Bankroll was busted . . = 56.997% of the time ( 569969)
Win goal was met . . . = 43.003% of the time ( 430031)
hmm
my matrix (recursion) in Excel
0.429755901 (at trial 2000)
hmmmm
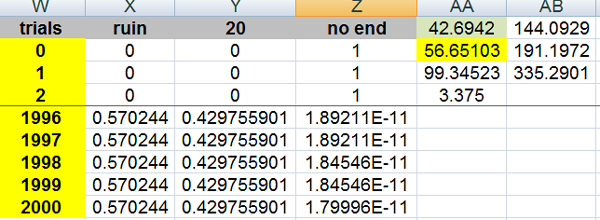
for the average # of bets and rolls for success or ruin (look at the above color photo)
totals: 99.34522596, 335.2901376
the expected number of trials for ruin or success can be calculated using simple recursion in Excel (as I showed)
and the formula for the expected number of trials for ruin or success by
Don Catlin (as does many stats and prob books too)
http://catlin.casinocitytimes.com/article/calculating-a-hold-percentage-1230
This one could be different on treating what is ruin as theQuote: AhighIf you bet $10 with 345x odds trying to win $100, you then have a 43.495% chance of success with an average of 21.22 rolls.
You have a 56.505% chance of failure with an average of 21.32 rolls.
unit bankroll is very small compared to the average unit bet of 34/9 (3 7/9) meaning a short session is in store here.
1) does the player bet everything on the pass line after losing enough to not make a full odds bet (namely betting bold) to get back to a bankroll level where full odds can be taken
or
2) does the player bet everything on the odds bet while not able to make a full odds bet and
3) player is ruined when bet is less than 1 unit
I used 2&3
same 1 million player simulation produced
Avg. No. games played . = 8.40
Avg. No. dice rolls . . = 28.35
Bankroll was busted . . = 56.268% of the time ( 562676)
Win goal was met . . . = 43.732% of the time ( 437324)
again, oh finally, we agree!
I may set up the matrix for this (345x odds) using a few different methods
to calculate the probabilities as I did for no odds
maybe not
Sally
Maybe not with the fortune and target shown.Quote: DrEntropyThis, it turns out is not true. See "Improving at Bold Play in Craps" by Ethier.
Basically Ethier showed that the (nearly?) optimal (in the sense of reaching a certain goal) is to bet the odds boldy, that is arrange it so that you are betting the maximum amount of odds consistent with not overshooting your goal and the rules of the casino.
care to show how this is done?
I can not do it without more study
Ethier's paper is quite advanced and his explanation in his book is about the same, IMO.
can it also be better with overshooting the target as what would happen in real play?
fun fun fun
summer time in SoCal
Sally
Quote: RSBecause for some reason, the Wizard and others think by placing a 0 edge bet it reduces your overall disadvantage & they calculate the edge of the flat bet and the odds together. Ridiculous.
May as well calculate BJ the same way (average $ in action vs average loss).
I don't think it's ridiculous, per se, I tend to believe it's just a question of perspective.
Argument in Favor: In terms of House Edge, if we assume a bettor is absolutely going to take Max Odds whenever he has the opportunity, then the PL + Odds can be viewed as a single bet, or Taking/Laying Odds, appropriately, can be considered Optimal Strategy if there is one. Much like doubling-down in BJ or occasionally making the 4x bet in UTH, it's not a bet that the player is forced to make, but it does lower the House Edge of the game.
Argument Against: This one is actually my opinion: While it is true that a player must have a Line/Come bet in order to make an Odds bet in the first place, the Odds bet is not a necessary bet and does nothing directly to reduce the House Edge of the money exposed on the Pass Line. Unlike UTH, where additional bets must occasionally be made to increase the overall return of good hands (thereby directly reducing the House Edge on the initial bet, as opposed to blindly checking all the way through and only making a Blind 1x bet at the end) the Odds bet has no affect on the House Edge of the Pass Line bet, as it is not a necessary component of the game. The money that was initially placed on the Line/Come bet will face the same House Edge regardless of future decisions, which isn't the case in games where a player gets additional money out because that improves the expectation of not only the additional money, but also of the initial bet.
what now?Quote: Mission146I don't think it's ridiculous, per se, I tend to believe it's just a question of perspective.
Argument in Favor: In terms of House Edge, if we assume a bettor is absolutely going to take Max Odds whenever he has the opportunity, then the PL + Odds can be viewed as a single bet, or Taking/Laying Odds, appropriately, can be considered Optimal Strategy if there is one.
Much like doubling-down in BJ or occasionally making the 4x bet in UTH,
it's not a bet that the player is forced to make, but it does lower the House Edge of the game.
you gave no Argument in Favor for a combined house edge IMO.
"I don't think it's ridiculous" so then is it useful?
Is it an easier value to work with? If yes, how about an example.
I truly do not see why it needs to be used at all.
I mean, we all can add ev values.
If I am going to make about 30 pass line bets over the next hour (a nice average)
and my bet without odds is $5 I stand to lose (my expected loss) 30 * $5 * -7/495 = -$X
# of bets*avg $bet* house edge = ev (-$X)
The Wizard
"The reason that the house edge is relative to the original wager, not the average wager,
is that it makes it easier for the player to estimate how much they will lose. "
I must agree here.
How about the expected loss for 345X odds and $5 flat bets. same 30 bets
combined House edge = 0.00374 (had to look it up too)
30 * $avg bet * -7/1870 = -$X
what is the average bet for 345x odds?
I am 100% certain that no one knows that value.
They need to look it up or calculate it or should I say just guess at it.
It should be $5 * (34/9)
-$X (ev) for both calculations should be the same
can one trust me on that?
what again is a good reason to know the combined house edge for the pass line and odds bet?
I still do not see any until I see one.
Sally
You sure are good at insulting me. It's no wonder you left the forum as you make plenty of mistakes. You just have not admitted to any mistakes that you have made that I have brought light to.
Starting with betting $50 a 4 or a 10 can come before a seven with a 1.00% house edge vig on the win buying the four and ten here in Vegas.
I predict you never admit any mistake related to this argument. I believe so because I believe you have a problem admitting that you made a mistake. Your refusal to admit you were wrong insults me and continues to insult me.
As far as deleting comments, I have been gone long enough, I didn't get know the rules had changed, and I thought the comments I made about you might insult you, just as yours insult me above.
Quote: mustangsally
-$X (ev) for both calculations should be the same
can one trust me on that?
what again is a good reason to know the combined house edge for the pass line and odds bet?
I still do not see any until I see one.
Sally
If my Argument in Favor of a combined House Edge did, in fact, suck, I can attribute that to the fact that my personal opinion is not in favor of a combined House Edge, as stated in my post.
In terms of utility, again, assuming a player who definitely WILL be taking Max Odds, the Combined House Edge will let him know what his Expected Loss is relative to the expected money exposed.
Again, I view them as two completely unique bets, one has a House Edge (resolved) of either 1.40% or 1.41%, depending on what side the player is playing and the other has a House Edge of 0%...that the former must be made (and the criteria of establishing a point met) in order to make the latter I don't consider relevant to the House Edge of the former.
So, are you trying to say for every $1000 wagered between the pass line and oddsQuote: Mission146In terms of utility, again, assuming a player who definitely WILL be taking Max Odds, the Combined House Edge will let him know what his Expected Loss is relative to the expected money exposed.
the player always taking 345x odds will have an expected loss of -0.00374 * $1000 = -$3.74, no matter their bet size.
Is this what you mean?
and the pass line with no odds player expected loss = -1.41% * $1000 = -$14.14, no matter the bet size. (my example before used $5 flat bets)
of course the time required on average to make that much in action is easy for the no odds player.
How many rolls or bets would it take for the 345x odds player?
A bit more challenging.
bottom lines
the expected loss for both players is the same over the same number of bets (same flat bet) and the same total $ of action.
one example in favor of using the combined house edge is what I now see when comparing equal action between two betting methods.
Sally
oh yes, from WinCraps
Another frequent use of this concept is to demonstrate the effect of taking or laying odds.
For instance, there are those who claim that odds bets do nothing to affect the outcome of the game.
They point out that if you bet $5 on the Pass Line you'll lose an average of 7.05 cents per decision (1.41% of your wager) whereas if you also take $10 odds you'll still lose an average of 7.05 cents per decision.
You're risking more money to lose the same amount, so why take odds?
Betting $5 flat on the Pass Line does not represent commensurate risk with betting $5 flat and taking $10 in odds. By adding $10 odds to the same $5 flat bet you're increasing your action. To figure the average action of $5 flat with $10 odds we have to consider resolutions on the come-out roll which produce only $5 action and resolutions after points have been established which produce $15 worth of action. Hence, 12/36 of the time the flat bet portion alone resolves on the come-out producing action of $5 * 12/36 = $1.67 and 24/36 of the time both the flat and odds bets resolve after points have been established producing action of $15 * 24/36 = $10. Add them together and we find that $5 flat/$10 odds produces an average action of $11.67 per decision. Now let's compare that to the $5 flat bet without odds.
It produces the same amount of action on every decision, so obviously the average action per decision is $5. So to make a fair comparison we can either reduce the $5 flat/$10 odds bets to something that produces an average of $5 action per decision or we can increase the $5 flat bet to something that produces an average action of $11.67 per decision. The later seems to be the easiest, so to make bets with commensurate risk we can compare $5 flat w/$10 odds to $11.67 flat without odds.
Now we can clearly see the effect of the odds bet because the $11.67 flat bet loses an average of 16.46 cents per decision which is much higher than the 7.05 cents per decision of the $5 flat bet with $10 odds.
The OP started out saying "Say I have a bankroll of $1000"Quote: AhighDid you assume my answers were wrong because you think you are smarter without even knowing what I did?
and your first post starts out
"If you bet $10 flat trying to win $100 with no odds, you will double your money 40.349% of the time with an average of 377 rolls.
Same strategy will lose the $100 buy-in 59.651% of the time with an average number of 361 rolls."
"you will double your money" is that part to me that was a what? moment
your answers are still not correct for the probabilities and the average number of rolls
please show your work on how you arrived at your answer.
I showed mine because being smarter than some one else does not matter.
some say it does.
The OP is very happy for all the *opinions*
Sally
And I've never understood why its a comparison of "no odds bet at all" versus "maximum odds", since few players really bet maximum odds and few players make an odds bet consistently each and every point. The odds bet erodes bankroll and many people consider the first thing to do when a bankroll is being seriously impaired is to quit making odds bets.
I don't think the 1.41 percent analysis is good methodology since no one ever wins or loses 1.41 on the pass line. I'd like to use five dollars as an example but lets be realistic and admit the lowest table you will find is probably a ten dollar table. If I lose my first three flat bets, I've lost thirty dollars. If I've made odds bets and lost I've probably lost sixty dollars. Ain't lost 1.41 ever.
Not all odds bettors make the bet as soon as the point is established. I wonder if this affects anything.
house edge used for expected loss is not for one bet onlyQuote: FleaStiffI don't think the 1.41 percent analysis is good methodology since no one ever wins or loses 1.41 on the pass line. I'd like to use five dollars as an example but lets be realistic and admit the lowest table you will find is probably a ten dollar table. If I lose my first three flat bets, I've lost thirty dollars. If I've made odds bets and lost I've probably lost sixty dollars. Ain't lost 1.41 ever.
it is an average BTW and one bet provides a very poor average value.
and any odds can replace max odds IMO
try 495 bets
many, if not all craps players make this many at least once in a lifetime and I am going to guess that they make it multiple times too.
If one only wins 244 out of 495 (the highest single probability outcome)
they will lose exactly the 1.41% (same average bets that is)
that happens, on average, for about 1 in 27.9 players that make 495 pass line bets (not at all astronomical against)
I am certain it happens every day (495 bet total is reached, not in one hour of play either)
but no one even notices because a computer does not track every bet they make and every result from making them
I feel many will have their own and different opinions on this too
more: OK try just 71 bets
win 35 and lose 36
happens in about 1 in 10.6
house edge = 1/71 (pretty and close to 1.41%)
Sally
Quote: FleaStiffWell, now I'm totally confused.
And I've never understood why its a comparison of "no odds bet at all" versus "maximum odds", since few players really bet maximum odds and few players make an odds bet consistently each and every point. The odds bet erodes bankroll and many people consider the first thing to do when a bankroll is being seriously impaired is to quit making odds bets.
I don't think the 1.41 percent analysis is good methodology since no one ever wins or loses 1.41 on the pass line. I'd like to use five dollars as an example but lets be realistic and admit the lowest table you will find is probably a ten dollar table. If I lose my first three flat bets, I've lost thirty dollars. If I've made odds bets and lost I've probably lost sixty dollars. Ain't lost 1.41 ever.
Not all odds bettors make the bet as soon as the point is established. I wonder if this affects anything.
At a $5 3-4-5X table, I often play max odds. It's not a bankroll busting-amount of money and I don't play continuous come or generally have a half dozen bets on the table. If you play the line and only the line (whether Pass or Don't) and you bet the table minimum on the come out roll, betting max odds is not that big of a deal.
My default playing style is to bet table minimum on the Don't, lay either max odds or sometimes 3-4-3X ($18 on the 6/8, $30 on all other points). If I find myself at a 5X or higher table, I'll usually stick to either 3-4-5X or 3-4-3X instead of betting the max. I would be tempted, on a $3 10X table, to bet 5-10-10X.
I don't think that always betting max odds is that rare, especially if the bettor is sticking to line bets.
Quote: mustangsallyThe OP started out saying "Say I have a bankroll of $1000"
and your first post starts out
"If you bet $10 flat trying to win $100 with no odds, you will double your money 40.349% of the time with an average of 377 rolls.
Same strategy will lose the $100 buy-in 59.651% of the time with an average number of 361 rolls."
"you will double your money" is that part to me that was a what? moment
your answers are still not correct for the probabilities and the average number of rolls
please show your work on how you arrived at your answer.
I showed mine because being smarter than some one else does not matter.
some say it does.
The OP is very happy for all the *opinions*
Sally
Run my simulation Sally. You can find any problems yourself, if there are any. I'm not going to lead you by the hand to where the source code is. It's clearly posted in my first response of this thread.
Your posts are ignorant of obvious things from the questions you ask and the statements you made, such as the statement implying that I didn't use a simulator.
I wrote a simulator from scratch for this post, Sally.
So far, you haven't even located the code.
"Use the source, Luke."
But check it out, I am done with you alright? It's clear you are obviously avoiding questions I am asking for a reason. Because you're obviously wrong.
Quote: AhighSally, did you see the source code I posted .
I personally have a hard time parsing perl. Your code is pretty clean, but I don't know where it goes wrong. But if you are flat betting (no odds) craps, the problem can be attacked with an analytic solution using the standard gamblers ruin formula:
(http://en.wikipedia.org/wiki/Gambler's_ruin) use the unfair game formula.
using n=10, p= 976/1980 we find probability of doubling = 0.4298
(We can use the ruin formula, because we are going to take our 10 units and either go broke or double it. So it is the same as if the casino only had 10 units as well, and they are 'ruined' when we double up.)
When you include odds bets, this becomes more complicated, and I would resort to simulation :)
Cheers!
Quote: DrEntropyI personally have a hard time parsing perl. Your code is pretty clean, but I don't know where it goes wrong. But if you are flat betting (no odds) craps, the problem can be attacked with an analytic solution using the standard gamblers ruin formula:
(http://en.wikipedia.org/wiki/Gambler's_ruin) use the unfair game formula.
using n=10, p= 976/1980 we find probability of doubling = 0.4298
(We can use the ruin formula, because we are going to take our 10 units and either go broke or double it. So it is the same as if the casino only had 10 units as well, and they are 'ruined' when we double up.)
When you include odds bets, this becomes more complicated, and I would resort to simulation :)
Cheers!
Quote: AhighIf you bet $10 flat trying to win $100 with no odds, you will double your money 40.349% of the time with an average of 377 rolls.
Same strategy will lose the $100 buy-in 59.651% of the time with an average number of 361 rolls.
So my sim reports 40.349% compared to 42.98%. That's close enough to indicate the sim is working and possibly I didn't run enough sessions for trials. In any case, hardly enough of a difference to warrant whatever attacks from Sally. But she has always had a problem with me for one reason or another. I suspect just from her being rather ignorant of the answers that I provide and focusing more closely to what she understands rejecting anything she doesn't.
Still I did misunderstand the problem where the OP wanted to know if he had $1000 and was trying to get a 10% increase to $1100, what was his chance of success, which is obviously much higher.
In any case, I'm a little less inclined to continue arguing with Sally. She has a history of refusing to make efforts to understand things outside of her domain of expertise. That includes Perl, and it includes bets that one can make that effectively are composed of multiple other bets (EG: betting that you can roll a 4 or 10 before a seven). I think she also has a hard time understanding how the pass line bet changes to a contract bet as well after the comeout.
more, just a little bit more complicated.Quote: DrEntropyWhen you include odds bets, this becomes more complicated, and I would resort to simulation :)
Cheers!
I mean, the math hack I am, I can do it almost in my sleep. (not in my head)
a 21x21 transition matrix in excel is all that is required
or just a 21 column recursion method because many find that method even way easier than excel and mmult()
I showed this earlier
IMO, those that live by simulations alone will also die from them too
there have been a few math guys (the Wizard included) that shows this formula to be used for doubling a bankroll
(I think SN Ethier even shows in his book how this is derived.)
=1/((q/p)^b_x+1)
where b_x = bankroll units
p = probability of success of one trial
q = 1-p
something learned?
Oh,
a=1
if a=b and b=c then a=c
no simulation or assembly required
Sally


