5 count

As has been reported, the correct use of the 5 count will reduce the amount wagered by
about 57%.... for most players that is one of the best tools you can use to keep your
head above water in craps.

Now as to its actual affect on winnings, that is difficult to judge. An example of
that is last Friday night, i had rolls of 7,2,1,1,1,27,1,19,18,1,37. Now the decent rolls
were good enough to provide a nice profit. Using a 5 count on me and others
saved me $360 on myself, because i did not lose alot on my short rolls. If you
start off with a 6 or 8 or a series of them your first 4 rolls, then it can cost you
some, but nearly as much as you save.

When i feel better i may only use the three count on myself and go to a come
bet on roll 3, with odds on 4.

Sometimes you get into a rut where it is all or nothing, then other times
you have decent medium rolls, and not as many 4/3....your betting should
match your results that evening.

At any rate waiting a couple of rolls before placing what ever bets you place
can be a good thing.

Dicesetter

deleted

If I played the light side, I would definitely use the 5-count or some sort of qualification mechanism. As a darksider, I happen to enjoy PSOs :-)

@dicesetter

Quick question what was the time duration (or just your time on the table that day) to complete all of those shots?

well thinking back i think i started about 4:20 friday and played until 6:30 maybe and we (wife was hungry) went to eat. The other 4 guys kept
playing. I got back at about 8 and they all went to eat so i had the table to myself until they got back, maybe at 9:30
give or take.

BY the time they got back i was tired and was nicely ahead so wife and i made our way home to my sofa where i
belong.

Dicesetter.

Quote: dicesitter

As has been reported, the correct use of the 5 count will reduce the amount wagered by
about 57%.... for most players that is one of the best tools you can use to keep your
head above water in craps.

I agree with you, and especially when playing at "higher" limits, I will use the 5-count to reduce my variance. I presume similar betting schemes that reduce your action would work as well, but the 5 count seems just fine!

Why not use a reverse 5-count? Why not be up on the come out roll, plus the next three or four rolls of the dice and then take down your odds plus all place bets, anticipating a 7-out? I think the average "hand" per shooter is 6 rolls of the dice.

But just think about how much money you could save employing the 15 count! All those losers you miss out on. And when those 16, 17, 18 roll hands occur, there you are fully across!

The "never bet on a random shooter" or the "infinity count" is better than the 5-Count; no doubt about that. The idea behind the 5-Count is simple, reduce exposure. It does not change the nature of the random game but for controlled shooters it allows them to stay at the tables, lose far, far less money on random rollers and bet the big bucks on themselves (everyone defines "big" in their own way). It also gets you into the game enough that it looks as if you are playing but cautiously.

What makes the 5-Count excellent is that it is a strictly mechanical system; no thought required. You do not study shooters or try to figure this or that out about shooters. You just apply the 5-Count. If you are trying to influence the dice on your turns too much thought is a terrible thing, it wastes way too much mental energy.

On random shooters I would recommend only betting one bet --- a Come bet with as much as you can afford in odds. The more numbers you bet at craps, the more games against the house you are actually playing and the more games against the house the more you will ultimately lose. So after the 5-Count, one Come bet, place odds and enjoy the game which has become your one number versus the seven; all other numbers are irrelevant. When other numbers come up it is only time passing, nothing more.

I don't think the reverse 5-Count would be as much fun. The long rolls would be missed. You'd also hang around on those long rolls and that would look somewhat nutty. The idea of "averages" is off base here.

Quote: AlanMendelson

I think the average "hand" per shooter is 6 rolls of the dice.

The average is actually 8.53 but I can't say I've ever witnessed a point 53. Possibly, Alan has.

Quote: FrankScoblete

Wow! What would the odds be on 23 sixes in 28 throws?

FrankScoblete, to what level did you press your 6 to during that roll? Did you employ the 5-Count ?

Jerry "Stickman" was shooting. Did not use the 5-Count on him. Had my six at table limit or close to it. I tend to go with my biggest bet right from the start on Stickman but I did begin moving it up as the roll continued.

Quote: cowboy

The average is actually 8.53 but I can't say I've ever witnessed a point 53. Possibly, Alan has.

Nah. But I was at a table at Caesars with six players... and the dice went around the table twice and each and every one of us had a point-sevenout. That's two point-sevenouts for each of us, and to tell you the truth a couple of guys might have a had a point-sevenout three times.

Do you think somone is going to attribute it to biased dice?

Quote: AlanMendelson

Nah. But I was at a table at Caesars with six players... and the dice went around the table twice and each and every one of us had a point-sevenout. That's two point-sevenouts for each of us, and to tell you the truth a couple of guys might have a had a point-sevenout three times.

Do you think somone is going to attribute it to biased dice?

Oooooh.....My kind of table.

Actually I like a super hot shooter better, but I see a lot more of this than that.

Quote: AlanMendelson

Why not use a reverse 5-count? Why not be up on the come out roll, plus the next three or four rolls of the dice and then take down your odds plus all place bets, anticipating a 7-out? I think the average "hand" per shooter is 6 rolls of the dice.

Alan, the median is 6 rolls.
A coin flip (almost 50/50) that the shooter will or won't make it past 6 rolls before a 7 out (the 7out is counted).
You can bet against your son on this each shooter for fun!

also more here about the 5 Count for those interested
http://forum.alanbestbuys.com/showthread.php?2845-Let-s-discuss-the-craps-quot-five-count-quot

So, I thought it would be fun for me, and I was right, to simulate and calculate the expected loss of some bets for the 5 Count against Alan's idea of 4 rolls and run.
I did not see this thread until after reading his other.
only the math results here and not a continued discussion of the many reasons to use or not to use the 5 Count.

Bottom line is Alan's "4 count and run" expected loss is less than the 5 Count, assuming all shooters are unskilled.

what follows is the method I used to arrive at that.

and we can easily compare different bets against each other when we know how many rolls on average we would be betting on.
I used a transition matrix in Excel to arrive at that and a few other answers.

SN Ethier in his Doctrine of Chances book (pages 515-516) has these two questions about the 5 Count.
I also found the answers in his answer pdf. (yes, I looked first at his answers before I calculated mine only after my simulation was run)

(a) Assuming an unskilled shooter, what is the probability that he will achieve the five-count?
(b) If one bets only on shooters after they have achieved the five-count,
what proportion of rolls does one bet on, assuming all shooters are unskilled?

some pics of my transition matrix in Excel.
Never fear (I-Q)^-1
and a few tables of data
yes, I will not show a detailed explanation on how to do these type of calculations here.
or my simulations.
That may follow in a future book.
A novel idea!

The X-Count and the Alan X- Count

X-count	probability achieve the X-count	proportion of rolls bet on	average # rolls bet on	proportion of rolls NOT bet on
3	0.689814815	0.585394641	4.990787982	0.414605359
4	0.595216049	0.504292728	4.299352797	0.495707272
5	0.513626686	0.434930249	3.708002274	0.565069751
6	0.443198803	0.375188685	3.198674963	0.624811315
7	0.382402499	0.323658322	2.759352324	0.676341678
Alan-X	probability achieve the Alan-X	proportion of rolls bet on	average # rolls bet on	proportion of rolls NOT bet on
3	1	0.338852317	2.888888889	0.661147683
4	1	0.429418081	3.66100823	0.570581919
5	1	0.507695219	4.328360768	0.492304781
6	1	0.575272278	4.904489677	0.424727722
7	1	0.633592644	5.401700547	0.366407356

This expected loss comparison to the Don Catlin 5 Count simulation
Place 6 & Place 8 always working
and replaced on a loss and taken down for the Alan-X count and run method

X-count	expected loss per shooter
3	-0.277265999
4	-0.238852933
5	-0.206000126
6	-0.177704165
7	-0.153297351
Alan-X	expected loss per shooter
3	-0.160493827
4	-0.203389346
5	-0.240464487
6	-0.272471649
7	-0.300094475

yes, I expanded the 5 Count to get values for other Counts as well as Alan's X Count and run

any errors here? I know of none.
I compared these to my simulations and I am happy.
Any errors one does find, please let me know. I could have messed up during a copy/paste
I was more interested in the method of how to calculate this than the actual results.

Sally

Quote: FrankScoblete

The "never bet on a random shooter" or the "infinity count" is better than the 5-Count; no doubt about that. The idea behind the 5-Count is simple, reduce exposure.

yes, but it is your other claims like

3) shooters who had developed a "rhythmic roll" that was an unconscious controlled dice shot; this through trial and error in the casinos

that gets the conversation going.

what I can not believe is Don Catiln, a math guy, saying this at
http://catlin.casinocitytimes.com/article/the-five-count-11842
"The next thing I addressed is the Captain's contention that the 5-count will find controlled shooters if they are at the table.
Here we come to a sticky point.
Some people claim that there is no such thing as a controlled shooter.
I can weigh in on this point. I have seen controlled shooters with my own eyes and have made money betting on them."
OK Don. Some take you words as a proof.

In the Christian world, many do find out that there really is no Santa.

Quote: FrankScoblete

What makes the 5-Count excellent is that it is a strictly mechanical system; no thought required.

As does Alan's 4 Count and run. 4,3,2,1 and run!

Quote: FrankScoblete

On random shooters I would recommend only betting one bet --- a Come bet with as much as you can afford in odds.

I would think the don't come/don't pass with odds would be the better bet

Quote: FrankScoblete

I don't think the reverse 5-Count would be as much fun.

I think it would be. Bet on every shooter.
Fun!

Quote: FrankScoblete

The long rolls would be missed.

Long rolls missed?
"simple, reduce exposure"
Are you missing the point of expected loss per shooter? The long and short rolls are factored in.

Quote: FrankScoblete

You'd also hang around on those long rolls and that would look somewhat nutty.

Looks can be deceiving.
Bottom line is to lose less on each and every random shooter.
"simple, reduce exposure"

Are you expressing a belief here in the Gambler's Fallacy?

Having Fun!
Sally Oh

No gambler's fallacy.

Because you are not betting until the 5-Count you will miss out on the early rolls in hands that will extend. But the 5-Counter will finally get on all extended hands. The bet all player will make money on repeating numbers prior to the 5-Count and will make a profit (I am assuming) as the hand goes past the 5-Count while the 5-Counter needs some hits to get into the black (assuming multiple bets and the same bets by both players). The bet-all player will be on the extended rolls from the very beginning. I'm guessing the loss to both players in a random game will be the same if the same total amount of money has been bet by each using the same betting scheme. In a truly extended run where a non-5-Counter only bet on 43 percent of the shooters by randomly selecting them he would be in the same situation as the 5-Counter.

A big BUT here: if the 5-Counter bets on only 43 percent of the rolls while the bet-all player bets on 100 percent of the rolls, the 5-Counter will obviously lose less money. If both bet the exact same amount on the same bets then I am guessing the losses will be alike. (I assume a large sample size.)

Also, couldn't the 5-Counter wait for the 5-Count and then do Alan's reverse 4-Count? Put up a Come bet or Pass Line bet. Wouldn't that be the same thing? So you eliminate five (or so) random rolls, bet on only four rolls after that and then take your bets down? Yes, the player would be on no extended runs but in a random game when all is said and done those long runs are meaningless.

Now, Alan is not betting that four decisions will be take place in a row without a seven. He is betting individual decisions. The 5-Counter is doing the same thing. Your simulation has that as its basis, yes?

As far as rhythmic rollers or dice controllers, if they don't exist that sentence has no meaning and therefore needs no analysis by you. If you think craps is strictly a random game all your calculations are for a random game. That's fine.

I asked on Alan's page if you could do the math for a 5-Counter who waits until the count is completed and then bets a Pass or Come to see what the expectation would be. (One bet is fine or more if you like.)

I enjoy your efforts.

Sorry Sally. Didn't realize you answered me on Alan's site.

Quote: FrankScoblete

Now, Alan is not betting that four decisions will be take place in a row without a seven. He is betting individual decisions. The 5-Counter is doing the same thing.

I used Don Catlin's $6 bets on the place 6 and place 8 in my simulations and calculations for the per shooter ev.
Had to keep the bets the same for that comparison.
I am sure that is not how Alan would play his 4 Count and Run
I had him make the bets on the new shooter, working for only the first 4 rolls if the shooter made it that far, replacing the bets on a winner 7 and keeping the same bet on a win. After the first 4 rolls - the 4 Count is reached, the bets are called off until the next shooter or are taken down.

that explains the 4,3,2,1 and run!

of course that probability of not winning or losing,
NOT having at least one decision using the Alan 4 count = (20/36)^4 = 0.0952598689 or about 1 in 11 shooters
The other 10 out of 11 shooters will see winnings and losses.
That is ACTION that players crave and it is just for a max of 4 rolls.
That is how it has a lower expected loss than the 5 Count does. just by a little but a little is good as a mile.

The proportion of rolls bet on using the 5 count as per my table = 0.434930249 (also Ethier's value)
For Alan's 4 Count = 0.429418081

Both values come from the average number of rolls to bet divided by the average number of rolls per shooter that = 1671/196
8.5255102040816326530612244897959 (win7 calculator)

Quote: FrankScoblete

I asked on Alan's page if you could do the math for a 5-Counter who waits until the count is completed and then bets a Pass or Come to see what the expectation would be. (One bet is fine or more if you like.)

I enjoy your efforts.

As explained at Alan's site, I really need to know the roll probability distribution.
edited 4/15:
using the lower 1/7 probability for the 7 and all other numbers increase exactly up the difference, I show in my matrix
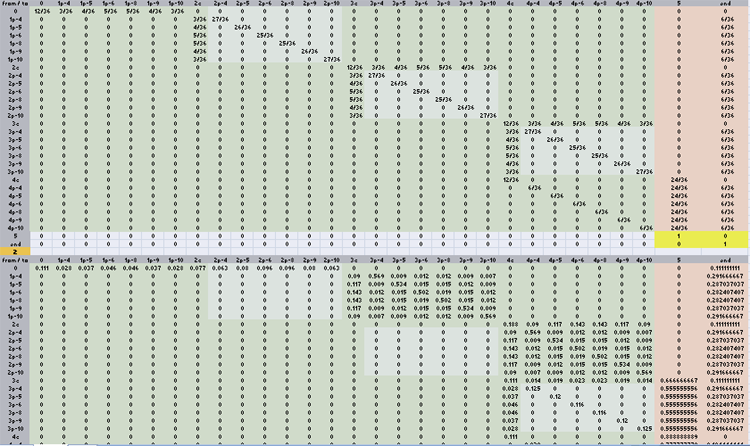
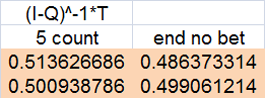
(I-Q)^-1*T
5 count
0.567471599 = probability achieve the 5-count
avg # of rolls per shooter not in the 5 count = 4.89473962

avg # of rolls per shooter to bet on = 4.757891959
9.652631579 = avg # of rolls per shooter with a 1/7 for 7
(higher than random at ~8.53 and was calculated and simulated. calculated value is shown)
proportion of rolls bet on = 0.492911381

I would have to calculate exactly the new transition probabilities after the roll probabilities are done first.
now I have a worksheet for it :)
that allows me to adjust from there once you come up with a roll probability distribution to use,
not just a 1/7 for the 7

I also did this in Excel using recursion and not any macros so any one can do this
or I can also link to my worksheet if interested.
Sally

I will keep future posts here too

added 4/15
I love color photos
my Excel recursion sheet.


a thought,
Really sad Don Catlin did not present data (maybe he did) that was calculated. Still very puzzling to me.
I found it so simple to do and less time than doing a simulation. (that was done also just to verify)
Also the makers of Smart Craps software does lots of shooter simulations too after making this remark about how difficult it is to calculate the probability distribution for the length of a shooters hand (how many rolls to 7out)
"It is possible to determine expected hand length for a random shooter via pure mathematics, but it requires
very complicated techniques."
http://www.goldentouchcraps.com/CrappyMath/math0004.shtml
and then shows a link to how Don Catlin calculated the distribution using a transition matrix.
The first method I used in Excel.
a simple recursion in Excel for the shooter's hand distribution for 1/7

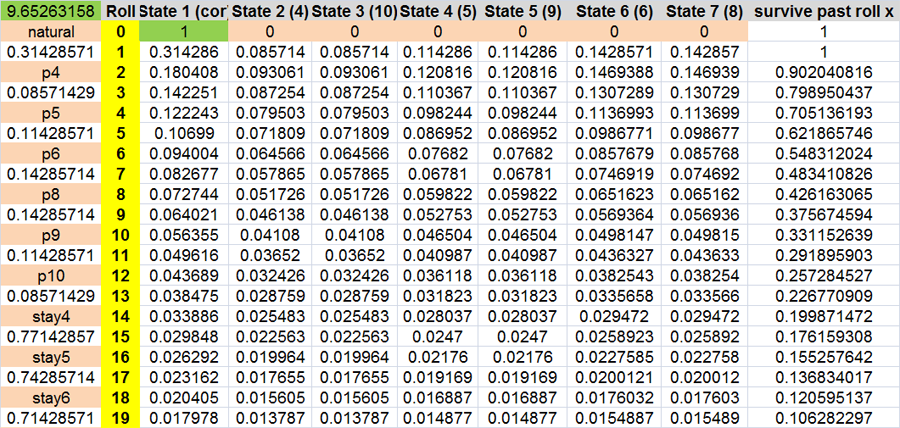
Simulations data contain errors that should be reported on how large they are. Most pass on this requirement (my opinion)

For Frank and or Smart Craps I do not mind at all sharing my work and worksheets.
This is so more can learn how things like this can be calculated and how simple they really are using simple programs that are available to most all.
Sally

Quote: FrankScoblete

In a truly extended run where a non-5-Counter only bet on 43 percent of the shooters by randomly selecting them he would be in the same situation as the 5-Counter.

added: I think I at first did not understand what you said above.
The ev for the 5 counter over 100 shooters = 100 * -$0.206000009 = -$20.60000085
The ev for a non-5-Counter over 43 shooters = 43 * -$0.473639456 = -$20.3664966

now the 5-Counter does bet on over 51% of shooters.
a shooter is more likely to pass the 5-count, no matter their SRR.
it is a 50/50 shot they do it by the 8th roll if they do it
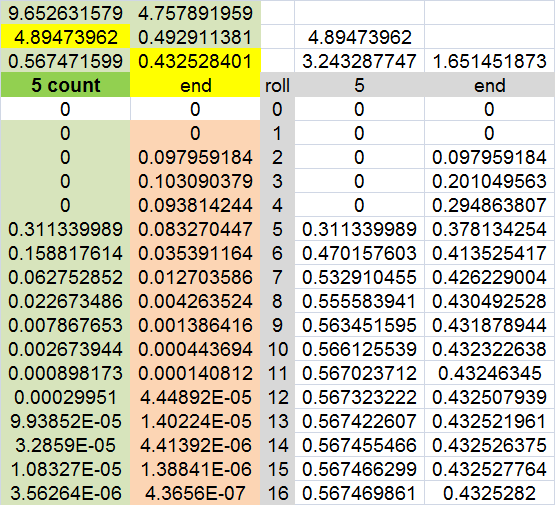
another table (from my Excel)
Col 1 and 2 is the probability of pass/fail on the Nth Roll.
Col 4 and 5 are cumulative (Nth or less)

5 count	end	roll	5	end
0	0	0	0	0
0	0	1	0	0
0	0.111111111	2	0	0.111111111
0	0.116769547	3	0	0.227880658
0	0.104766804	4	0	0.332647462
0.273319616	0.091223629	5	0.273319616	0.423871091
0.144678837	0.039791436	6	0.417998453	0.463662528
0.059828005	0.014827739	7	0.477826457	0.478490266
0.022767292	0.005203234	8	0.50059375	0.483693501
0.008356869	0.001777854	9	0.508950619	0.485471354
0.003012585	0.000599858	10	0.511963204	0.486071213
0.001075022	0.00020116	11	0.513038227	0.486272372
0.000381145	6.72543E-05	12	0.513419372	0.486339626
0.000134516	2.24516E-05	13	0.513553888	0.486362078
4.73054E-05	7.48946E-06	14	0.513601193	0.486369567
1.6587E-05	2.49742E-06	15	0.51361778	0.486372065
5.80123E-06	8.32628E-07	16	0.513623582	0.486372898
2.02438E-06	2.77568E-07	17	0.513625606	0.486373175
7.0499E-07	9.25271E-08	18	0.513626311	0.486373268
2.45059E-07	3.08431E-08	19	0.513626556	0.486373298
8.504E-08	1.02812E-08	20	0.513626641	0.486373309
2.94645E-08	3.42707E-09	21	0.513626671	0.486373312
1.01941E-08	1.14236E-09	22	0.513626681	0.486373313
3.52222E-09	3.80787E-10	23	0.513626684	0.486373314
1.21547E-09	1.26929E-10	24	0.513626685	0.486373314
4.18956E-10	4.23097E-11	25	0.513626686	0.486373314
1.44252E-10	1.41032E-11	26	0.513626686	0.486373314
4.96171E-11	4.70108E-12	27	0.513626686	0.486373314
1.70501E-11	1.56703E-12	28	0.513626686	0.486373314
5.85373E-12	5.22343E-13	29	0.513626686	0.486373314
2.00803E-12	1.74114E-13	30	0.513626686	0.486373314

You always mix up the percentage of shooters that achieve the 5 count and
the percentage of rolls that are bet on per shooter.
It is all over the internet.
"Because the 5-Count eliminated approximately 57 percent of the random shooters"
just one example from:
http://goldentouchvideopoker.net/WeeklyArticles/45.shtml

I guess you did not find my posted results for this at all interesting or maybe even accurate.
I mean I do disagree with Don Catlin's results that you have in some internet articles
as I have calculated them instead of just doing a simulation. (I did both)
I still agree with SN Ethier's calculated results as I posted earlier.

random rollers
probability to achieve the 5-count = 0.513626686
percentage of shooters that achieve the 5-count =51.3626686%
So, the Captain was right in thinking that about 50% of shooters would pass the 5 count.
probability NOT to achieve the 5-count = 0.486373314

proportion of rolls to bet on = 0.434930249
percentage of rolls to bet on = 43.4930249%
percentage of rolls NOT to bet on = 56.5069751%

Quote: FrankScoblete

A big BUT here: if the 5-Counter bets on only 43 percent of the rolls while the bet-all player bets on 100 percent of the rolls, the 5-Counter will obviously lose less money. If both bet the exact same amount on the same bets then I am guessing the losses will be alike. (I assume a large sample size.)

now this sounds much better, but how do they bet the exact same amount or have the same total action?
It is all about the average number of rolls that are possible to bet on.
that is where the percentages come from.
See my data tables
-0.206000126 = the expected values from place 6 & 8 for the 5 count (still using Don Catlin's parameters)
from 3.708002274 = the average number of rolls to bet on after the 5 count
The average shooter has =1671/196 average rolls 8.525510204
That is how the BetAll players has an expected value of -0.473639456 per shooter
= 1671/196 * -2/36

Don Catlin's simulation error = 0.000125166
but has a much higher error for the 5-Count player of 0.002036686
my simulation error is way smaller, but am not interested in that as much as these values can easily be calculated.

Quote: FrankScoblete

Yes, the player would be on no extended runs but in a random game when all is said and done those long runs are meaningless.

yes, meaningless.
So you really should stop saying one will miss the long rolls by a shooter.
It is all about the average number of rolls that could be bet on.
There are no long rolls by a shooter, it is already in the probability distribution for the length of as shooters hand.

BTW, I also have calculations for the "wait only rolls" that are in other articles over at GTCraps.
Especially the wait 7 rolls being equal to the 5 count.
This is all incorrect.

the ev for that for the wait 6 rolls and now start betting = -0.201167807
LESS than the 5 count
I should start another thread for that too.
The internet is full of articles with wrong information.
That is just not right.
Here is a table for the X-Wait Count
expected loss is again for the place 6 and place 8 bets only

Xwait-count	probability achieve the X-count	proportion of rolls bet on	average # rolls bet on	proportion of rolls NOT bet on	expected loss per shooter
3	0.772119342	0.661147683	5.636621315	0.338852317	-0.313145629
4	0.667352538	0.570581919	4.864501974	0.429418081	-0.27025011
5	0.576128909	0.492304781	4.197149436	0.507695219	-0.233174969
6	0.49721087	0.424727722	3.621020527	0.575272278	-0.201167807
7	0.429044107	0.366407356	3.123809657	0.633592644	-0.173544981

BTW2, the most common roll to 7out on = 3
this is true for the 1:6SRR and the 1:6.5SRR (using the hardway set all times) and the 1:7SRR shooter
and in order for all 3
3,2,4,5,6,7,8,9,10,11

that would be a topic for another thread.
I have data and calculations for that too, unlike just simulation data, that contains errors, that have been shown in articles by the Smart Craps folks.
I am 100% certain they do mean well

Sally
now back to work

You have to realize that the five count is nothing more then a sales gimmick, meant to booster sales of Frank's craps school. It does absolutely nothing for you, now he can throw up all the numbers he wants to, and show you all the percentages. But the truth of the matter is, every time there's a new shooter there is no way of telling if they are going to get past two rolls the dice!

Basically you are using a mechanical system that has no way a telling if the shooter will make it past six roll the dice! Then you have to also look at, the math of the game, which says most players will never get pass eight rolls of the dice!

People that are trying to sell you something love to confuse you with facts and figures, the only problem is, they leave out the most important ones! Like most people never make it pass eight the dice!

What they managed to do with just five count was, piss off every casino there is, with players waiting five rolls of the dice before they make their first bet, you have to remember that casinos make their money off of rolls per hour. The way they look at it is, if you're standing there and not betting you are costing them money!

Just imagine when a school parades all of their students into one casino and they take over the tables and using the five count that they just learned. If you've ever been in Vegas and had the misfortune of being at a craps table when they descended on it like a swarm of locusts playing musical shooters as they swapped out shooters in SL1 and all of them using the five count, you could see why a casino wouldn't want any so-called DI's playing on their tables!

These schools love to use the gimmick of having all of their students taking over a table, and trying to put on a show, it's nothing more then a advertising gimmick for them. Sometimes one of their students do manage to get on a roll, and it might sell someone else on taken their class.
You have to remember, if they all are losing you wouldn't even notice them at the table, they would all be standing there, with sad little faces and empty chip racks! There would be no screaming and shouting!

Don't kid yourself into using a five count, evaluate the players that you want to bet on, don't let a mechanical system do it for you. After all,.. By now everybody should know that systems do not work!


_________________
Note, all my post start with this is just my opinion...!

You do good brada ..!

superrick

Winning comes from knowledge and skill when your betting and not reading fiction!

The five count is harmless, I see nothing inherently "wrong" with it.

Conceptually, it seems to achieve its goal of avoiding early PSO's, if only because the player is out of action during the early part of a roll.

Of course, it does nothing to increase a player's odds of winning: that is the important thing to remember.

All craps players have an approach to the game, a method of play; whether you start every shoot by betting $160 across, or $10 don't pass, we must all choose SOME way of betting, and that's all the five count is: an arbitrary method of play.

Me, I prefer to place six and eight and progress and spread out a bit if a roll heats up; Frank prefers the five count.

We each handle the reality of craps in our own way.

Now, now supperick, the 5-Count came 12 years before I ever taught a dice control class.

On my last visit to Hollywood casino in Columbus, Oh, I witnessed three tables packed with players, most bet with full odds and across. Some people won $500-3000. They came to gamble, not to save hard earned money. Really, what's point to travel across the country if you go to Vegas and try to save. You can do it by collecting coupons, when shopping at your local grocery.

Quote: MrV

Frank prefers the five count.
We each handle the reality of craps in our own way.

Frank also wants to be noticed as the one that introduced the Captain's 5 Count to the world.
That must make him feel real good.

In this video

he says at 4:52
"the five-count is the only shooter selection system
that has been proven to work in a massive study of 200 million shooters"

Well, move over 5 Count, you ain't the only one. Others work as well or even better.
I have shown two other systems that do actually better than the 5 count.
The Alan 4 count and run and
the 6 roll count and bet

It also says this on youtube
"The 5-Count will save you money, get you in on long rolls and help you get more comps."

In an earlier post I showed that there are no such things as long rolls.
That is included in the length of a shooters hand probability distribution.
All short and long rolls are included in that distribution.

Here is another article that comes to a wrong conclusion over at Golden Touch Craps
The 7 count because the 5 count may be too hard to count.

"My friend knows the 5-count but prefers to count rolls instead."
http://www.goldentouchcraps.com/skinny0006.shtml

"We know from another of Dr. Catlin's studies 57% of random shooters do not make it past the 5-count."
This is NOT true. another misunderstanding of simulation data.

I and SN Ethier calculated that the 5 count
probability achieve the 5-count = 0.513626686 or about 51.4%
So about 48.6% of random shooters do not make it past the 5-count

What the 5 count actually does is bet on *less rolls on average per shooter*
proportion of rolls bet on = 0.434930249 or about 43.5% meaning on average 56.5% of rolls are not bet on.
Not 57% of shooters are not being bet on.
Of course it is very possible using the 5 count that the very next 5 shooters will all fail to make it past the 5 count.
such is the nature of random events.

I show the stats on the X-roll count and bet system in another post for those so interested.

The 6 roll count (then bet) and the Alan 4 count (and stop betting until next shooter)
has a lower expected loss per shooter than does the 5 Count. (making the same $ bets and type of bets)

now more choices (shooter selection system) betting on random rollers.
Sally Oh

Sally, can you point me to the discussion about the Allan 4 count and the 6 roll count method you mention in your above post?
Thank you.

Quote: eclectic

Sally, can you point me to the discussion about the Allan 4 count and the 6 roll count method you mention in your above post?
Thank you.

That is a great post that Sally wrote. You should read it. But to summarize, if you stay out of craps action for 4,5,6 or any number of rolls, you will lose less money. You will not win, you will simply lose less.

But the original post by SuperRick says about the same thing. Read that also.

Im not sure what to think about the 5 count, but I do know that it seems every roll that starts out with lots of craps rolls (3,3,11,2) very very seldom turn out to good rolls!

Tks! much for your efforts and response DeMango. I just also found this on a previous page.

https://wizardofvegas.com/forum/gambling/craps/14166-5-count/

Here's my dilemma or perhaps lack of understanding on these stats.

Alan's 4 Count. I can't find it now but I thought that somewhere the Wizard come up with 3.2 as the ______________number of rolls?
Meanwhile there is this article showing 3.37 rolls.

https://www.dicecoach.com/articlearch.asp?ID=47

So, wouldn't you be at risk waiting for those 4 rolls? And since the Wizard/Catlin came up with 8.53 as the average number of rolls wouldn't the shooter also be at risk by betting after 6 rolls; or especially the 8th as shown here?

http://www.goldentouchcraps.com/article.php?p=skinny0006.html

Why not wait for the 9th roll? I know it looks kinda long in the tooth, but.......

Tks for any feedback.

I GOT IT!!! 3 MINUTE ABBS....

The odds of the 7 never change for the random roller, always 1 outta 6. It all adds up to 8+ rolls, including come out, for everybody since the beginning of time.

DeMango, I'm spending some time in the tall weeds on this subject as you suggested. Can you clarify a detail for me please? As is obvious according to the 5-Count Rule, the shooter starts the count after the appearance of the 1st Box number rolled, and ends when the 5th Box number is rolled. The rules state that the shooter begins betting on the next roll after that criteria has been met. Now, if I am correct, Sally's testing method regarding her 6-Count method is that the shooter begins betting on the 7th ROLL of the dice, and whether the rolls are box numbers or other than box numbers (2,3,7,11,12) is immaterial? Is that correct? Many thanks again for your perspectives and helping me understand Sally's math.

Well since the 5 count goes back to the writings of the famous gaming author Scoblete who invented all sorts of things, and saw all sorts of things (but not 18 yo's in a row), the best thing would be to buy one of his books, used, for 10 cents plus shipping. (I really do not want you to waste too much money.) In it he will lay out his rules for the 5 count. There are his certain rules but I never wasted my time with them. Same goes for Sally, though I assume her's is a straight count. Bottom line is the more you stay away from betting the less you lose. And that is all you need to know.

of all the stupid assinine things written about craps over the years, the 5 count takes the cake.

DeMango, thank you for responding. Iv'e already purchased most of his books and yes it has definitely occurred to me that even playing craps for profit might be a total waste of time which could have been used for currency towards different hobbies or projects.

I was just wanting to insure I understood correctly. I believe Sally's 6-Count is based on 6 ROLLS of the dice, and that roll 6 does not have to be a box number. Unless I have misunderstood, that is what I see in her post.

Yeah, those books are a bargain, (:-)

Sally, could I implore you to respond?

Meanwhile, all the best.

The only comment I would have is that I don't agree with the scuttlebutt that Craps is a simple game. It's not. Yes, one can assume, or make it simple, but to arrive at a a personal betting strategy: (who to bet on, what to bet, when to bet, how much to bet, etc.) takes some time to develop. As an example, I am taking the liberty of posting something all of you are probably familiar with by Heavy. I know,...I know....please hold your negative comments. Being a newcomer, it took a lot time to process the explanations of his play. Most of you guys can execute all this without thinking. I believe there is a lot of wisdom in his post, although I can't agree to the totality of his strategy. It's just an example. Notice how he employ's AMs 4-Count Sally came up with? Perhaps his play is based on experience, but as the old saying goes, a moment of insight is sometimes worth a lifetime of experience. My best.

http://www.dicesetter.com/heavy/heavy8playbook.htm

A shooter qualifier is mandatory with these dice nowadays. Whether one count or 5 count for place betters. I like increasing odds bet as box numbers rolled on each point sequence, concentrating on odds bet with its 0 house edge just may be our best chance.

you people need to look up the word random in the dictionary and try to understand it....then all this qualifier nonsense would quietly go away.