What if Aces can only be 11s? (Hypothetical Thought experiment)

I'm wondering what would change with the math of the game if Aces are only allowed to be 11? Very curious, but I lack the math/programming capabilities to simulate it.

To clarify:

Ace would no longer count as 1 for either the player or the dealer, it would only count as 11.

An A and a T is still a blackjack, and still pays 3:2

There will be no more soft hands, an A7 for example would be a hard 18. And you probably don't want to double any hand with an ace.

If you have a hard 16 and draw an Ace, that is a bust, not a 17

Same goes for the Dealer. If the Dealer has upcard 5, hole card A, draws a 7, they don't get to keep drawing, that's a bust.

And the unfortunate special scenario that I must decide a ruling on: Pair of aces

And this is my ruling, which I think would be fair.

If the dealer has A and flips over a hole card A, that's a bust

If the player has AA, the player will be offered an opportunity to split Aces. If the player cannot afford or does not want to split, the hand is a bust and loses.

If on the split, another Ace is dealt, the player may split again. If either player has already reached split maximum, or resplit aces is not allowed per house rules, that specific AA hand is a bust and loses.

All other rules same as standard blackjack.

I have many curiosities what would happen in this hypothetical game. Such as:

- What would be the house edge on the game?
- How does basic strategy change if Aces can only be counted as 11?
- Is the Hi-lo counting system still the overall "best" system?
- Does the rule change make Hi-lo counting system perform even better than it does on the standard blackjack game?
- What will be the changes to the Hi-lo indexes? I'm guessing probably 16v10 would have its tipping point to stand at a much more negative count, instead of TC0.


A bit into my thought process of how I came up with this thought experiment:

I was thinking about the hi-lo counting system. Where in terms of EOR, aces are lumped with tens as high cards.

However, in terms of play, Aces sometimes behaves as a 1/11 hybrid, sometimes it can only be a 1 (11 would bust the hand)

For example in 16v10, any additional ace is forced to be a 1. Even though, the Hi-lo deviation lumps it with tens. But I think it behaves much more similarly to a 2 than to a 10. In other words, more aces being previously out makes the hand decision lean more towards stand, rather than hit. Despite more aces being dealt out means a lower True count.

Also imagine doubling a 11 and getting an Ace. The effect of this Ace is nearly identical to 2,3,4,5,6, and opposite of 10.

So I'm a bit uncomfortable with the Hi lo system counting Aces as high cards. From a EOR perspective, they are very similar to 10s, and that's fine. But from a playing deviation perspective, many, possibly even most of the time, they behave like a small card rather than a 10. Causing me to think many of the hi-lo deviations are dubious since it lumps Aces and Tens together.

That's what led me to this thought experiment, of what the blackjack game would look like if we force Ace to always be a big card.

I'm hoping in digging through the math together, it would shed some light on how to think of Aces in hi-lo deviations. Therefore bringing pragmatic benefits to this otherwise completely hypothetical thought experiment.

It is a weird proposition and I have no idea how to run a sim for that.

In regular blackjack, double down of 12 has a 4/13 chance of busting so we don't do that.

In this blackjack, double down of 11 would have only 1/13 chance of busting. Is it possible that 11 vs. 6 could still be a double even with chance of losing it all?

You are effectively removing all soft doubles as well as many soft hits for the player (A4 vs. 2 and A6 vs. 7-10 and the like).

I have to think the house edge is increased in this game and the new basic strategy would kind of be all over the place compared with what we know.

How about this- whoever gets the first up Ace decides if it's an eleven or a one. Whatever he chooses, it affects all the Aces in the game. If he counts it as eleven, all Aces are counted as eleven. Until the next Ace appears and that player can keep them all at eleven or change them all to ones. Players only, and whatever the holder of the last Ace dealt chooses, applies to the dealer. If a player has an up Ace and declares it a one, no one can score a blackjack. If the dealer turns over a two-handed blackjack, it is not an automatic winner as a player can still draw an Ace and declare it is a one.
If the player has a blackjack but is forced to count the Ace as one and draw another card, he can double down. If he doubles down and draws a ten-value card for a three-card 21, it pays 2-1.
Half blackjack and half follow the queen, the fact that this game introduces the ability to screw over the rest of the table should make it popular.

You surely would not hit a hard 16 vs Ten, maybe not 16 vs 9.

You might stand on all hard 12 vs 2-6.

Using the Wizard's "BS Using Excel" youtube video for infinite decks with surrender, I generated this BS table for "Hard Ace BJ":



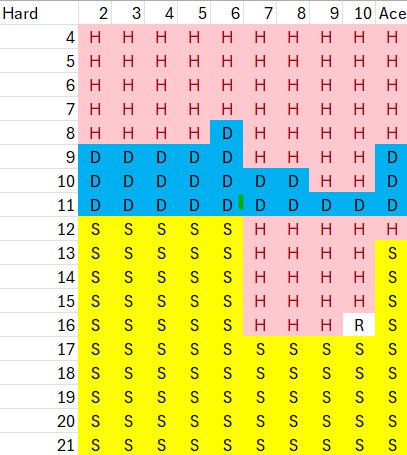
If surrender is not available, 16 vs. 10 is a Stand with EV = -0.5013.

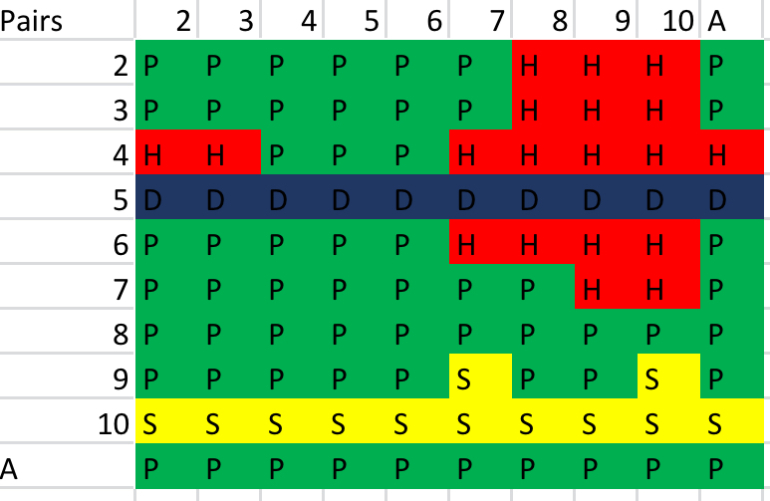
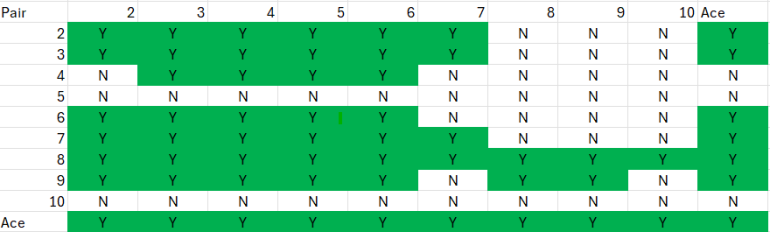
Here is the splitting strategy:



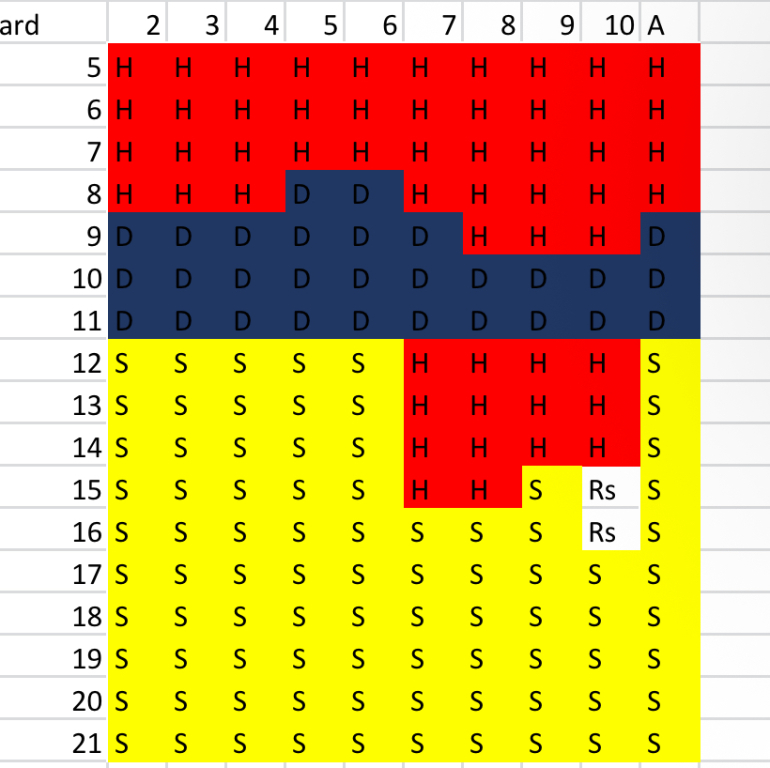
For reference, here are the dealer outcomes for when the dealer does NOT have a BJ:



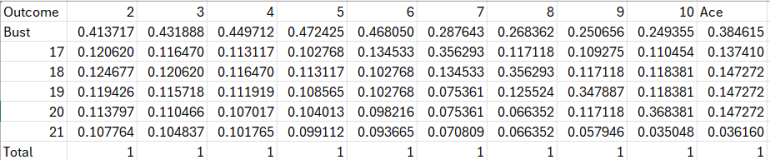
Note that when the upcard is an Ace, the dealer busts nearly 38.5% of the time.

Before the dealer checks for BJ, here are the outcomes for 10 and Ace up:



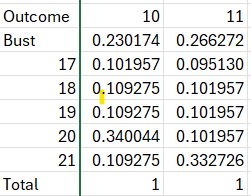
Hope this helps!

Dog Hand

Interesting. Color me surprised that one always doubles 11 even with that 1/13 chance of busting the double down. That's wild.

Any chance you can calculate the house edge on this game? Really not a big deal as this is all a silly curiosity experiment.

(double post)

I’m getting a slightly different basic strategy:
I’m getting the same dealer outcomes