DEALER: Insurance is open
JOE GAMBLER: Are you kidding me? Never take insurance, it's a sucker's bet!
DEALER: Okay, insurance is closed. No one's home. You have 15
JOE GAMBLER I stay.
Little does he know, our friend Joe should expect to lose less money if he takes insurance and then hit his 15 if the dealer has no blackjack. That's cool but what other egregious mistakes do blackjack players make? With the help of Wizard's Blackjack Hand Calculator I've created a basic strategy chart showing only the 2nd best option for strategy. All of the filled-in cells show the play that is so bad, you are expected to lose more money than you would on an insurance bet, 7.4% of it. White-filled cells are within 0.074 of a bet of each other. Here's a standard basic strategy chart for reference
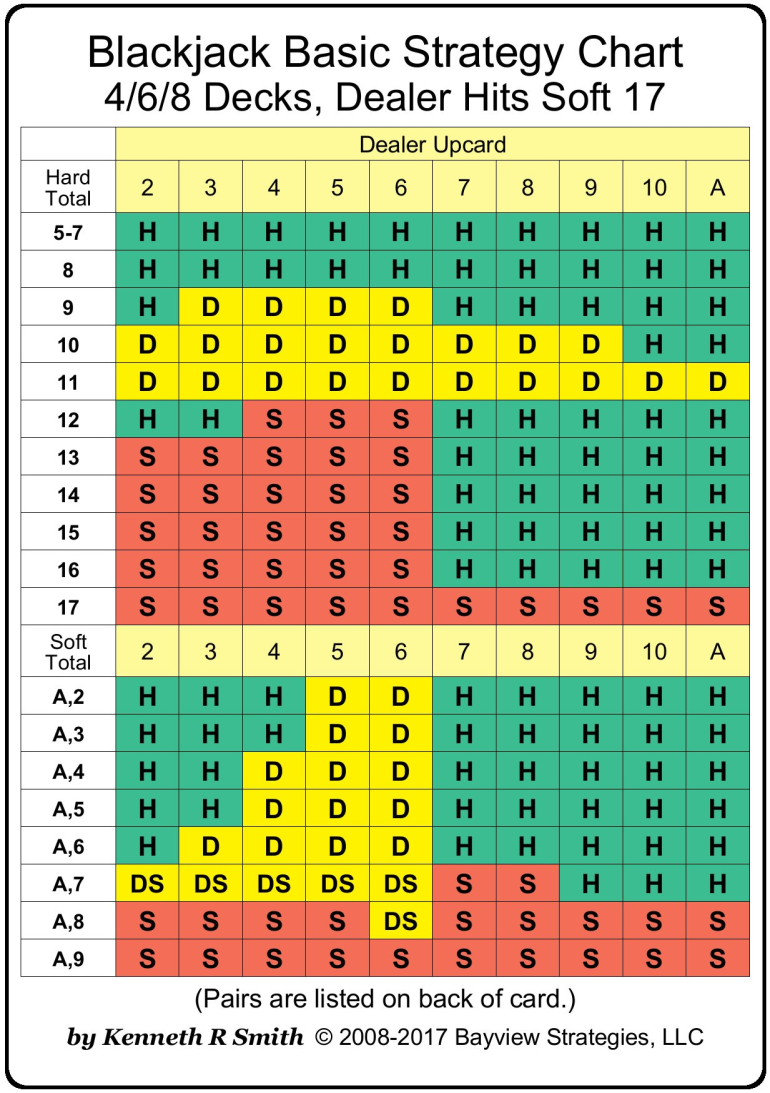
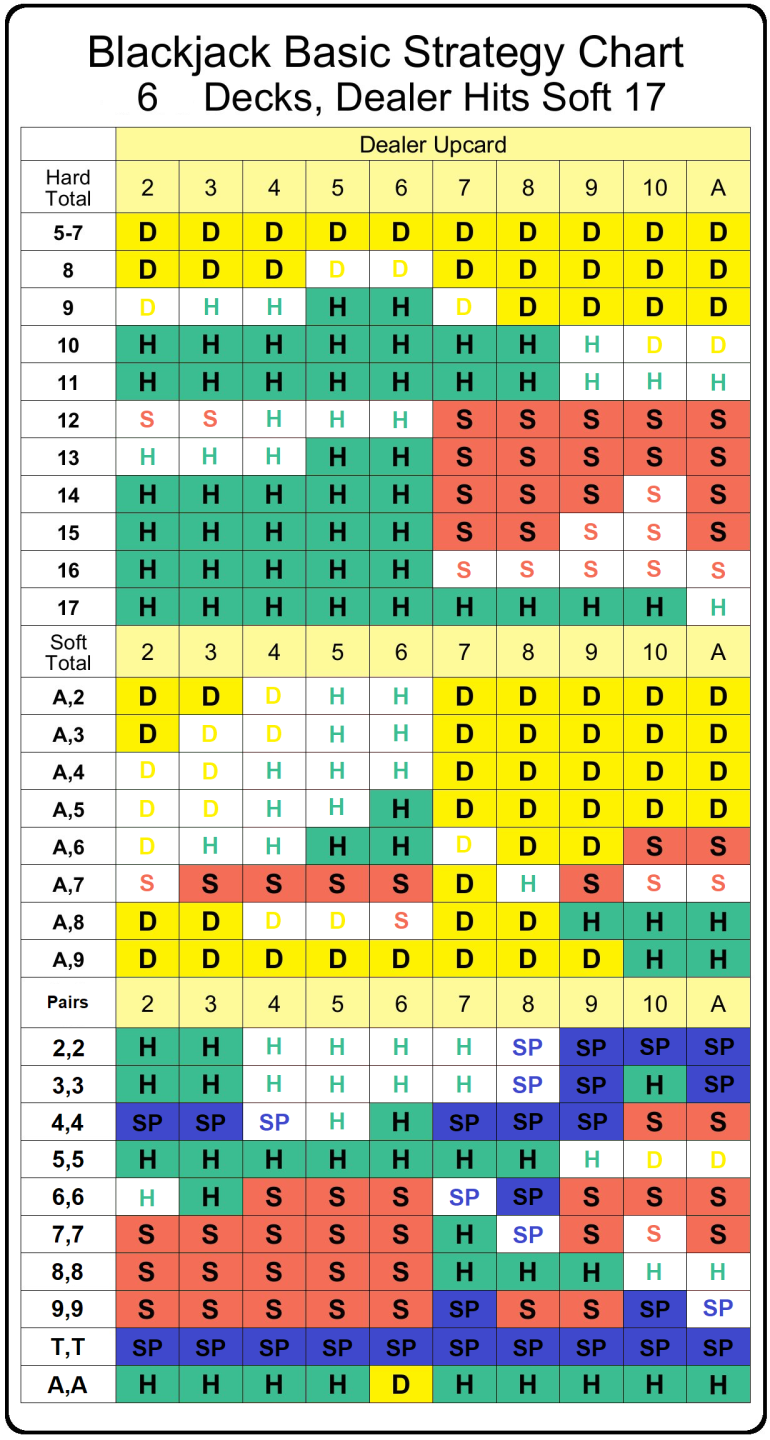
Studying the chart, you'll be surprised not only to find just how bad some plays are, but how not-so-bad some others are like 12v6 or 17vA. Hope some of you find this as interesting as I did!
Quote: richodudeHow bad are some people's blackjack strategies exactly? Let's first paint the picture
DEALER: Insurance is open
JOE GAMBLER: Are you kidding me? Never take insurance, it's a sucker's bet!
DEALER: Okay, insurance is closed. No one's home. You have 15
JOE GAMBLER I stay.
Little does he know, our friend Joe should expect to lose less money if he takes insurance and then hit his 15 if the dealer has no blackjack. That's cool but what other egregious mistakes do blackjack players make?
link to original post
The decision on taking of insurance is not complex math: It Pays 3:2. Therefore if there are > 1/3 of the unseen cards with 10 value, then take it. If not, don't. The default proportion is 4/13 =0.308 which is why generally you won't. Cards dealt and seen go into the calculation, but other than that, don't change the insurance strategy
With 15 he should have hit unless he has extra knowledge.
The insurance decision should be independent from the hand play decision. Why would you want to play the second best choice?
Quote: OnceDear
The decision on taking of insurance is not complex math: It Pays 3:2. Therefore if there are > 1/3 of the unseen cards with 10 value, then take it. If not, don't. The default proportion is 4/13 =0.308 which is why generally you won't. Cards dealt and seen go into the calculation, but other than that, don't change the insurance strategy
With 15 he should have hit unless he has extra knowledge.
The insurance decision should be independent from the hand play decision. Why would you want to play the second best choice?
link to original post
You seem to be missing the point. This is not some new-fangled strategy but merely to show how ironic it can be when a blackjack player will refuse to take insurance but happily makes any of these second-best plays without realizing how much worse than insurance they are. I deal blackjack for a living so it is pretty relevant to me
Yes. I missed your point. Sorry.Quote: richodudeQuote: OnceDear
The decision on taking of insurance is not complex math: It Pays 3:2. Therefore if there are > 1/3 of the unseen cards with 10 value, then take it. If not, don't. The default proportion is 4/13 =0.308 which is why generally you won't. Cards dealt and seen go into the calculation, but other than that, don't change the insurance strategy
With 15 he should have hit unless he has extra knowledge.
The insurance decision should be independent from the hand play decision. Why would you want to play the second best choice?
link to original post
You seem to be missing the point. This is not some new-fangled strategy but merely to show how ironic it can be when a blackjack player will refuse to take insurance but happily makes any of these second-best plays without realizing how much worse than insurance they are. I deal blackjack for a living so it is pretty relevant to me
link to original post
With some plays, the second best choice is a hairs breadth difference. But with other variations, the user could be really messing up. Thus we learn basic strategy. Your mention of taking insurance confused me. Insurance is a separate decision.
Interesting idea, and nice graphic for 2nd best basic strategy (2BBS).
Which 2BBS play is closest to actual BS in terms of EV?
Dog Hand
Surrender is notably better, of course.
Regarding this online calculator, I noticed one important function is not working properly as it used to do. The deck composition numbers have been grayed out for some time and thus I cannot select an arbitrary card number of a certain card rank.
I posted this problem to Wizard in another thread, but hasnít heard back anything about this.
Quote: DogHandrichodude,
Interesting idea, and nice graphic for 2nd best basic strategy (2BBS).
Which 2BBS play is closest to actual BS in terms of EV?
Dog Hand
link to original post
Good morning! I remember 2 that were very close, A2 v 5 with a difference of 0.00341 units for doubling and hitting. I canít remember the other Iíll try and find it later. All calcs were done with 6 decks before the hand was dealt
Quote: acesideWhy do you list a Hit decision for 33 v T? Shouldn't it be Stand?link to original post
Standing will never be better than hitting (under normal circumstances) for any hand of hard 11 or less (or for that matter a soft hand of 16 or less).
Quote: acesideThe A7 v 2 Double/Stand decision is very close too. Why do you list a Hit decision for 33 v T? Shouldn't it be Stand?
link to original post
Dangit, I knew thereíd be one. Yes, the second best play is to stand on your 6 rather than split or double down. That also reminds me of the other super close strategy decision which is between the 2nd and 3rd best play for this hand. Standing will only win you 0.00476 more of a unit than splitting. Of course, neither of these plays are even close to just hitting
For regular Black Jack:
If I'm running a progression, I may take insurance if I have a Black Jack against a Dealer Ace if I'm just trying to rack up a win to advance in the progression and not merely tie and go nowhere. But that's usually when I'm a few or several bets into the progression.


