Thread Rating:
| Net Win | Probability | Return |
| -8 | 0.00000019 | -0.00000154 |
| -7 | 0.00000235 | -0.00001643 |
| -6 | 0.00001785 | -0.00010709 |
| -5 | 0.00008947 | -0.00044736 |
| -4 | 0.00048248 | -0.00192993 |
| -3 | 0.00207909 | -0.00623728 |
| -2 | 0.04180923 | -0.08361847 |
| -1 | 0.40171191 | -0.40171191 |
| -0.5 | 0.04470705 | -0.02235353 |
| 0 | 0.08483290 | 0.00000000 |
| 1 | 0.31697909 | 0.31697909 |
| 1.5 | 0.04529632 | 0.06794448 |
| 2 | 0.05844299 | 0.11688598 |
| 3 | 0.00259645 | 0.00778935 |
| 4 | 0.00076323 | 0.00305292 |
| 5 | 0.00014491 | 0.00072453 |
| 6 | 0.00003774 | 0.00022646 |
| 7 | 0.00000609 | 0.00004263 |
| 8 | 0.00000066 | 0.00000526 |
| Total | 1.00000000 | -0.00277282 |
i.e., house edge of -0.277282%
I tried to use that data to calculate the RTP another way: $ returned to player ÷ total amount bet. For each line where we didn't lose, I tally the $ the player was paid, plus getting their non-losing bet back. First I'll show how that would look with a -simple, made-up game:
| Net Win] | Probability | Return |
| -1 | 0.51 | -0.51 |
| +1 | 0.49 | +0.49 |
| Total | 1 | -0.02 |
i.e., 2% house edge.
We could get the same result by looking at only the non-losing bets, plus getting our money back on those bets:
| Net Win] | Bet returned | Raw return | Probability | Return |
| +1 | +1 | 2 | 0.49 | 0.98 |
| Total | 0.98 | |||
i.e., 98% of money returned to player.
But that method doesn't work with the blackjack data:
| Net win | Bet returned | Total | Probability | Return |
| 0 | 1 | 1 | 0.08483290 | 0.08483290 |
| 1 | 1 | 2 | 0.31697909 | 0.63395818 |
| 1.5 | 1 | 2.5 | 0.04529632 | 0.11324080 |
| 2 | 1 | 3 | 0.05844299 | 0.17532897 |
| 3 | 1 | 4 | 0.00259645 | 0.01038580 |
| 4 | 1 | 5 | 0.00076323 | 0.00381615 |
| 5 | 1 | 6 | 0.00014491 | 0.00086946 |
| 6 | 1 | 7 | 0.00003774 | 0.00026418 |
| 7 | 1 | 8 | 0.00000609 | 0.00004872 |
| 8 | 1 | 9 | 0.00000066 | 0.00000594 |
| Total | 0.50910038 | 1.0228 |
For starters, the probability of having a non-losing hand is positive, so it seems that it's not possible that we're gonna see a house edge in this game. And indeed, the return shown is 1.0228, a 2.28% player edge.
I'm thinking that the reason for the discrepancy is that blackjack is special in that you can lose more than the original bet (e.g., a loss of -8 if you split 3x to 4 hands and double each one). Classic calculation for BJ house edge is relative to the original wager only, not any extra $ you put down for doubles and splits. So, my conclusion is that my method would work for most other games, but not in a game where you can lose more than your original bet. Does that seem right?
When there is net payout of +8, he is providing the probability or frequency with which the following has occured:
- player is dealt a pair that is split and resplit until he has four separate hands
- each of the four hands is then doubled (after split)
- each of the four doubled hands wins versus the dealer's hand
- your net outcome after this action is that you are +8 units wealthier than you were before the action
When there is a net payout of -8 units, the identical action has occured- you have split and resplit to 4 hands and doubled each of the four hands - but each of the four doubled hands has lost to the dealer's hand and you lost a total of 8 chips.
So, when you win or tie the value of the "net payout" already includes the return of your original wager.
But does the +8 really include the return of the original wager? If you make a bet and split to 4 hands, that's 4 units wagered. If you double each of those, you've now wagered 8 units. If you win all of those, then you're +8 from where you started. In addition to that +8, you also get back everything you put on the table (8 units).
As I said in my OP, with a similar table to the Wizard's for a simple game, I can look at the winning line(s) only to figure the return, but that doesn't work with the blackjack table, and I'm thinking the reason is that blackjack is special in that you can lose *more* than the original wager.
You cannot determine the number of bets at risk from this table. Therefore, you cannot determine the net W/L divided by the money put at risk.Quote: MichaelBluejayI'm thinking that the reason for the discrepancy is that blackjack is special in that you can lose more than the original bet (e.g., a loss of -8 if you split 3x to 4 hands and double each one). Classic calculation for BJ house edge is relative to the original wager only, not any extra $ you put down for doubles and splits. So, my conclusion is that my method would work for most other games, but not in a game where you can lose more than your original bet. Does that seem right?
link to original post
Just look at the line for 'Net Win' = zero. This represents a large number of hands where you simply push plus a large number of hands where you double and push or split and win one and lose one hand. Also, it includes a smaller number of hands where you spilt/double to four bet units and get back four units, etc.
At no place in this table does the Wizard provide information regarding these partial probabilities. I assume he calculated them separately in his work product, but just chose not to display them here. If you knew what the subfractions were, then you could calculate the denominator for ROI.
Two lines where you know the amount of money at risk are the +8 and -8 lines. These are purely the result of winning or losing all bets with 8 units bet. I think +7 and -7 are also pure. The other lines are a mixture of different numbers of bets at risk.
The amount put at risk is arbitrary. He's showing eight decimals. Okay, then $100,000,000 @ $1/round would cover the whole table.Quote: MentalYou cannot determine the number of bets at risk from this table.
How do you figure? My conclusion was the opposite: He *did* include those hands. e.g., Split once, one hand win, the other loses, that's a net of zero, showed on the Net Win = 0 line.Quote: MentalAt no place in this table does the Wizard provide information regarding these partial probabilities. I assume he calculated them separately in his work product, but just chose not to display them here.
Though no one is addressing my conjecture directly, it seems more and more to me like the reason I can't add the positive lines (like I can with the other game) is because blackjack is screwy in that you can lose *more* than your original wager.
UTH and betting progressions are also examples where more than one unit is bet.
When the (0 - 1) is not the right value to use in the expectation value calculation, your formulation breaks down.
Any game, including blackjack and craps, can be easily expressed in a binary “p(lose 1) or (1 - p) win x” format exactly matching the variance and edge of the actual game. I believe this is what OP is attempting
With a SD of about 1.15, blackjack is actually a low variance game, relatively speaking. The SD of passline plus 3-4-5 odds or a single roulette number are 4 or 5 times higherQuote: ChumpChange0.50910038 - 0.08483290 = 0.42426748 = 42.43% chance of winning anything per deal. YMMV wildly per shoe.
link to original post
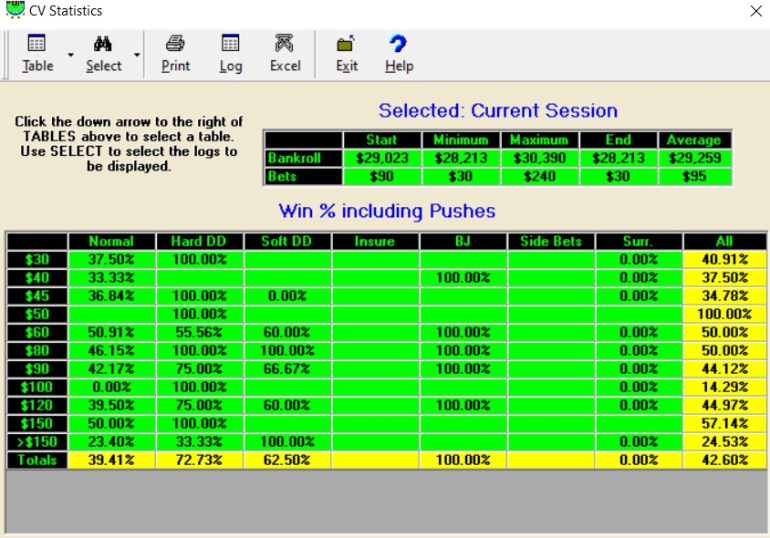
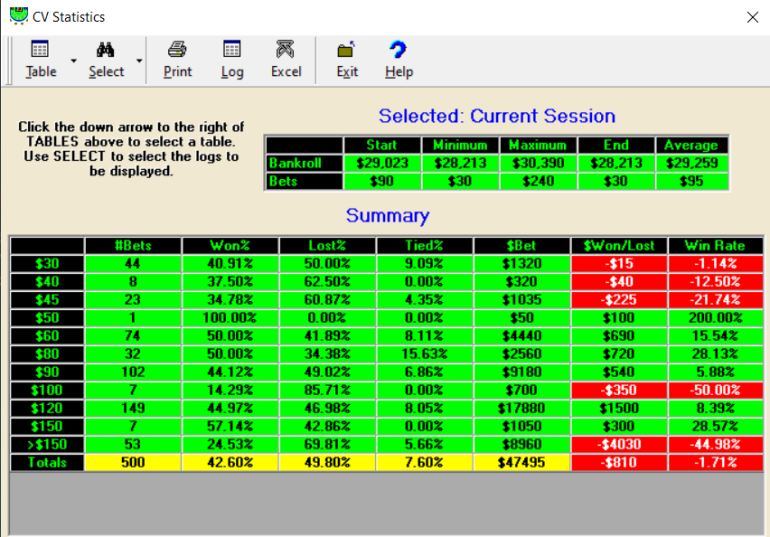
So I'm winning 42.60% of hands and tying on 7.60% of hands, and losing on 49.80% of hands.
But I'm only winning 39.41% of my normal hands and losing on my hard double downs 27.27% of the time and losing my soft double downs 37.50% of the time. I've been getting really bad beats on my splits to 3-4 hands with at least 1 double down. I play hard to get 10 units ahead, then comes the sucker play where I lose 4-8 units on bad splits and double downs, over and over.
I'm averaging 300 hands per hour playing one on one on the computer. I expect 200 hands per hour playing heads up at the casino, but more like 50 hands per hour at a full table.
I started this game with $100K, but the machine defaulted me down to $30K. So I'm playing $1,000 sessions to start off with $25-$5,000 table limits.
And yet another example of losing on the splits and double downs and ending my session.
HE and RTP are expressed as a fraction or percentage. HE = 1 - RTP. RTP clearly has numerator and denominator. RTP = bets returned divided by bets put at risk. Expectation value is not a fraction. It is calculated over one PDF. That PDF could have a basis of one unit bet or it could have a different basis or no basis. You can have an expectation value for a drawing where you bet nothing.
EV only equals HE when one unit is put at risk. So, you are right in that sense.
In craps, you can calculate EV by only looking at the line bet. The odds bets don't affect EV. They do affect RTP or HE.
Every time I’ve tried to explain something, your response is something like “my math skills don’t go beyond basic arithmetic” with the implication that you have no interest in improving that. When I recently suggested you use a simple Markov chain for the RoR calculation in another thread, your response was “but I have no idea what that is”. Well…google it, study it and work out some examples until you figure it out. Seems you just want someone to give you formulas and then you throw them at a problem without actually understanding what you’re doing (this thread being one of several examples)Quote: MichaelBluejayOkay then, care to explain?
link to original post
I have never written a BJ calculator. I would expect that the house edge would be based on all money wagered. I often play BJ online with around 0.5% cashback. I get paid this cashback on all wagers. I use the RTP posted in the game rules with a crosscheck with the calculator at blackjackinfo. Clearly, my edge would be even higher than I calculate if MBJ was right.Quote: MichaelBluejay... Classic calculation for BJ house edge is relative to the original wager only, not any extra $ you put down for doubles and splits. ...link to original post
I think the quoted assertion is wrong. I think the calculators use all wagers in the denominator. I would appreciate an expert weighing in on this important question.
If you use all money wagered as denominator then it’s called “element of risk”, a term coined by Wizard as I recall
https://en.wikipedia.org/wiki/Gambling_mathematicsQuote: Ace2Based on initial wager only
If you use all money wagered as denominator then it’s called “element of risk”, a term coined by Wizard as I recall
link to original post
The house edge (HE) or vigorish is defined as the casino profit expressed as a percentage of the player's original bet. In games such as Blackjack or Spanish 21, the final bet may be several times the original bet, if the player doubles or splits.
This sounds like the expectation value expressed in units of the initial bet. If this is industry practice to call this a percentage when it only a percentage of an arbitrary unit, then I will have to adapt to this sloppy terminology. I see why Wizard thought we needed a new term, but I wish he had chosen something better than element of risk.
The house edge defined in this manner is of no direct use to me.
Let’s say you play a blackjack game with a HE of 1/2% and SD of 1.15 for ten hours at an average 50 bets per hour. Your expectation is -2.5 units +-/ 25.7 units.
From that you can project your variance off expectations with any level of confidence you like and also get an accurate RoR for any bankroll amount. Some bets will end up being more than the original bet amount, but how is that relevant to anything?
I get cashback on every bet. If I know the house edge as a percentage of initial stake, it is useless to me for determining my edge. I need the RTP calculated over all bets to decide if a promo is worthwhile.Quote: Ace2Mental,
Let’s say you play a blackjack game with a HE of 1/2% and SD of 1.15 for ten hours at an average 50 bets per hour. Your expectation is -2.5 units +-/ 25.7 units.
From that you can project your variance off expectations with any level of confidence you like and also get an accurate RoR for any bankroll amount. Some bets will end up being more than the original bet amount, but how is that relevant to anything?
link to original post
I just finished 2000 bets of BJ for a promo. I had milestones along the way. I decided to quite after 750 bets based on my tiny edge for the remaining bets. Then the casino added a loss rebate so I finished the 2000 bets. Note that I don't care about hands per hour, just bets per hour.
I understand why table players might think in terms of expectation value per hour, but APs are jumping their bets up and down all day and taking breaks when the count goes south. Their true edge is always changing. Can an AP really get the expected win and variance from the single bet EV? Not at all.
I did a quick estimate and the expectation value of a hand expressed in starting bet units is at least 12% larger than the actual hold as a percentage of the amount wagered.
It is an expected value. It has to have units. I believe it is expressed in units of a starting bet. I am very clear on what is going on here. I went to the Wizards page linked in the OP. It is a nice article. It calculates EV, not the ambiguous house edge. Wizard does not say what units he uses, so I am assuming units of one starting bet.Quote: Ace2I think you’re confused. It’s not “single bet EV”…it’s the expect value of your play of a specific number of hands, regardless of how many units are bet after the initial bet. The EV and SD factor in everything including splits doubles etc
link to original post
I think you are muddying the waters by talking about " expect value of your play of a specific number of hands". I understand it to be the expected value of one starting hand played to completion using optimum strategy. How many hands do you think it covers?
https://wizardofodds.com/games/blackjack/appendix/9/euro-8ds17r4/
The EV is not for one hand. It is calculated over all possible results summed over all hands played off of one starting hand.Quote: acesideI'm not sure what the argument is, but EV is just for one hand. However, it is averaged over all possible outcomes.
link to original post
EV is use less for me. I have no risk of ruin. I had a balance of 200,000 bets for the play I just finished. I care not about variance. Explain to me why I should care about the EV of the hand. My decision is based on my edge, and the EV does not figure into my edge.
For any calculation involving probability, you need at least hundreds of trials/hands to have any sort of confidence of your actual result being close to your expected result
All calculators definitely use the initial wager as the unit for RTP and House Advantage and Player EV. This is the universally accepted convention.
If Mental or others have needs for other metrics to take optimal advantage of loss rebates or freeplay, than great! Proceed to calculate them.
But my real average bet was $70 and my total bet was $153.5K and my total loss was $5.9K at -3.83% W/L. I just need to win 30 hands ahead to wipe out the deficit of $6K, but how often is that going to happen at any point during the first 10,000 hands, or even the next 500 hands? I know it's possible to get that far ahead in less than 150 hands, but when will it happen?
That's not accurate.Quote: Ace2Every time I’ve tried to explain something, your response is something like “my math skills don’t go beyond basic arithmetic” with the implication that you have no interest in improving that....Seems you just want someone to give you formulas...
(1) I *do* have some skills beyond basic arithmetic.
(2) I've improved my math skills many times by things I've learned on this forum, and from the Wizard.
(3) In my OP, I didn't ask for a formula. I suggested if my idea of the *concept* was correct.
(4) The RTP table is done with simple arithmetic. Tell me with a straight face that the explanation requires a Markov chain.
Responding to my original post with only "That seems all wrong" is just ridiculously unhelpful.
It also seems inaccurate. Based on what I posted, it does indeed seem that the reason for the discrepancy vs. the other game I posted about is, as I stated, that in the case of blackjack, it's possible to lose more than the original bet (upon which the return is based). You think that's "all wrong"? You certainly haven't offered a compelling explanation of why it's supposedly wrong.
Thanks for your expertise on industry conventions. I note that Wizard uses expected value with implied units of the initial wager amount. My go-to calculator is blackjackinfo. For some misguided reason, they express their results as a percentage: For example., "8 decks, H17, DAS, No Surrender, No Peek: Estimated casino edge for these rules: 0.80 %". I just assumed this was return/wagers which is unitless because a percentage is a unitless metric.. I was wrong. I might not have made the wrong assumption if blackjackinfo had omitted the '%' sign.Quote: gordonm888The EV based on units of the initial bet is the universally accepted metric because it is relevant to the decision of whether you want to play that game, whether you want to make that first wager on that game. Additional wagers, such as splitting and doubling on based on the expectation that those decisions are optimal at the time that those decisions need to be made (based on EV as a metric).
All calculators definitely use the initial wager as the unit for RTP and House Advantage and Player EV. This is the universally accepted convention.
If Mental or others have needs for other metrics to take optimal advantage of loss rebates or freeplay, than great! Proceed to calculate them.
link to original post
I can probably get by with a single correction factor to convert EV to a house edge percentage estimate. The doubling and splitting rules are fairly universal in my universe, H/S17, Peek, and Surrender rules vary but should make much difference.


