https://www.wolframalpha.com/input?i=∫+%281%2B1%2Fx%5E4%29%5E0.5+dx+
Quote: ThatDonGuyFirst thought: rewrite it as (sqrt(x^4 + 1) / x^2) dx, then see if you can integrate it by parts
link to original post
Thanks for your reply. I agree that we can rewrite it to (1+x^4)^0.5 / x^2
The hard part is (1+x^4)^0.5, which I can't figure out.
I would appreciate if someone could show me the solution step by step.
Quote: ssho88Quote: ThatDonGuyFirst thought: rewrite it as (sqrt(x^4 + 1) / x^2) dx, then see if you can integrate it by parts
link to original post
Thanks for your reply. I agree that we can rewrite it to (1+x^4)^0.5 / x^2
The hard part is (1+x^4)^0.5, which I can't figure out.
I would appreciate if someone could show me the solution step by step.
link to original post
I don't have time to work this out,, but let me suggest the following: When using integration by parts you need to find the integral of (1+x^4)^0.5. Try setting x^2 = tan y with (2x dx ) =sec^2(y)dy. Thus, (1+x^4)^0.5 dx becomes sqrt(1 + tan^2(y))* (1/2*tan2(y))/sec^2(y)dy.
However, (1+tan^2(y)) = sec^2 (y) so sqrt(1 + tan^2(y))*(1/2*tan2(y))/sec^2(y)dy =
1/2*tan-2 (y)dy. That should be integrable, I imagine.
I hope I didn't make a mistake . . . .
You mentioned : "Thus, (1+x^4)^0.5 dx becomes sqrt(1 + tan^2(y))* (1/2*tan2(y))/sec^2(y)dy."
With substitution x^2 = tan(y), I get :-
(2x dx ) =sec^2(y)dy, and x = sqrt(tan(y))
dx = (1/2) * (1/x) * sec^2(y)dy
(1+x^4)^0.5 dx = sqrt(1 + tan^2(y)) * (1/2) * (1/x) * sec^2(y)dy
= sqrt(1 + tan^2(y)) * (1/2) * (1/sqrt(tan(y))) * sec^2(y)dy
= sec(y) * (1/2) * (1/sqrt(tan(y))) * sec^2(y)dy
= sec^3(y) * (1/2) * (1/sqrt(tan(y))) dy
= ????
It does not have an elementary anti-derivative.
Quote: ssho88Thanks gordonm88,
You mentioned : "Thus, (1+x^4)^0.5 dx becomes sqrt(1 + tan^2(y))* (1/2*tan2(y))/sec^2(y)dy."
With substitution x^2 = tan(y), I get :-
(2x dx ) =sec^2(y)dy, and x = sqrt(tan(y))
dx = (1/2) * (1/x) * sec^2(y)dy
(1+x^4)^0.5 dx = sqrt(1 + tan^2(y)) * (1/2) * (1/x) * sec^2(y)dy
= sqrt(1 + tan^2(y)) * (1/2) * (1/sqrt(tan(y))) * sec^2(y)dy
= sec(y) * (1/2) * (1/sqrt(tan(y))) * sec^2(y)dy
= sec^3(y) * (1/2) * (1/sqrt(tan(y))) dy
= ????
It does not have an elementary anti-derivative.
link to original post
yes, sorry, I typed that out quick before running out the door. I've been gone all day, until this moment. The basic idea with the substitution x^2 = tan y was to reduce sqrt(1 + x^4) to a simple trigonometric expression, while accepting whatever you get for dx. I guess it didn't work out but I don't know any other way of attacking an integral with a term sqrt(1 + x2n).
Can we pursue an antiderivative of X = sec^3(y) * (1/2) * (1/sqrt(tan(y))) by using sec^2(y) =tan^2(y) + 1 ?
X = 0.5*sec(y) *(tan^2(y) +1)/tan^(-0.5)(y) = 0.5* sec(y)*tan^(1.5)(y) +0.5*sec(y)*tan^(-0.5)(y)
This form of X might possibly have an anti-derivative with an analytic form. It is a sum of two terms that are both of the form sec x * tana.
Only a very few functions have a closed form for their anti-derivative expressible in elementary functions. I have no idea if what you've posted is such a function, but it smells like one to me. Wolfram Alpha says the anti-derivative needs a "hypergeometric function."Quote: ssho88∫ (1+1/x^4)^0.5 dx = ?
link to original post
y=1/x, dy/dx= -1/x^2
(ds)^2 = (dx)^2 + (dy)^2
ds = dx * (1+(dy/dx)^2)^0.5 = (1 + 1/x^4)^0.5 dx
s = ∫ (1+1/x^4)^0.5 dx .
Then I got stuck here.
ETA: Wait a minute… The “length of curve, f(x) = 1/x”. Without citing boundaries (boundless), wouldn’t that be infinite?
I did notice that the integral of (1/sqrt(a2+u2) = arsinh (u/a) + C This is the closest form that I have found for a simple integral relevant to your problem.
Also, the integral of(1/(u*sqrt(a2+u2)) = arcsch |(u/a)| + C where I think arcsch is an arc-hyperbolic cosecant.
All of which seems to be in sync with teliot's comment about Wolfram's advice to look at hyperbolic functions. However, hyperbolas have different mathematical properties than the curve you are studying and I'm not sure if they will reduce to your curve by, say, setting the distance between the two foci to 0.
Certainly not an "easy math problem."
Quote: gordonm888Recognizing that this was either an unsolvable integral (i.e., no analytic form for the anti-derivative) or at least one for which the solution is not widely known, I was just typing in notes in my posts as I studied it. I realized that my posts were not directly helpful, sho88, I was just trying to come up with a good idea on how to start the analysis.
I did notice that the integral of (1/sqrt(a2+u2) = arsinh (u/a) + C This is the closest form that I have found for a simple integral relevant to your problem.
Also, the integral of(1/(u*sqrt(a2+u2)) = arcsch |(u/a)| + C where I think arcsch is an arc-hyperbolic cosecant.
All of which seems to be in sync with teliot's comment about Wolfram's advice to look at hyperbolic functions. However, hyperbolas have different mathematical properties than the curve you are studying and I'm not sure if they will reduce to your curve by, say, setting the distance between the two foci to 0.
Certainly not an "easy math problem."
link to original post
Possible to solve this problem with Taylor series ?
Taylor series, (1+y)^0.5 = 1 +y/2 - y^2/8 + y^3/16 - (5*y^4)/128 + (14*y^5)/256 +. . . . . .
For my case, just replace y with 1/x^4 . . . .then the integration will be very easy !
Any comments ?
For a numerical approximation, this is exactly what I would do.Quote: ssho88
Possible to solve this problem with Taylor series ?
Taylor series, (1+y)^0.5 = 1 +y/2 - y^2/8 + y^3/16 - (5*y^4)/128 + (14*y^5)/256 +. . . . . .
For my case, just replace y with 1/x^4 . . . .then the integration will be very easy !
Any comments ?
link to original post
Quote: gordonm888Nice. But with y = x^4, is there any convergence issue when x<1?
link to original post
Convergence issue is my concern too. Thanks for your comment.
Quote: teliotFor a numerical approximation, this is exactly what I would do.Quote: ssho88
Possible to solve this problem with Taylor series ?
Taylor series, (1+y)^0.5 = 1 +y/2 - y^2/8 + y^3/16 - (5*y^4)/128 + (14*y^5)/256 +. . . . . .
For my case, just replace y with 1/x^4 . . . .then the integration will be very easy !
Any comments ?
link to original post
link to original post
Thanks for your comment.
However, I think that series only converge if -1 < x < 1. So I think still not able to find length of arc 1/x from x = 1 to x = 3. Any comment?
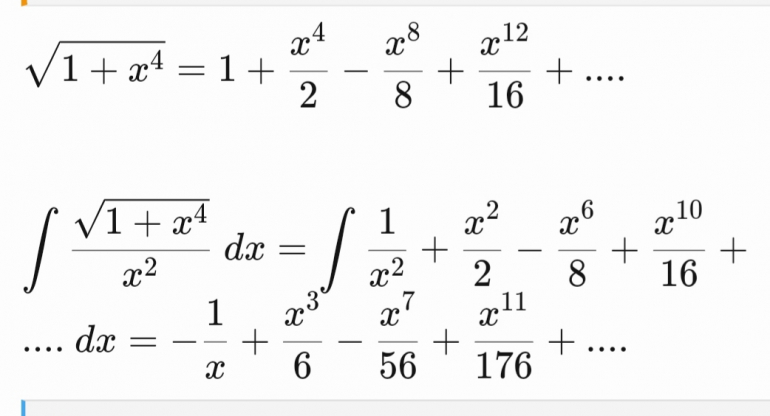
Quote: ssho88Here is the integral solution:-
However, I think that series only converge if -1 < x < 1. So I think still not able to find length of arc 1/x from x = 1 to x = 3. Any comment?
link to original post
Just the same comment I made twice before.
https://www.wolframalpha.com/input?i=arc+length+1%2FX&assumption=%7B%22F%22%2C+%22ArcLength%22%2C+%22a%22%7D+-%3E%221%22&assumption=%7B%22F%22%2C+%22ArcLength%22%2C+%22b%22%7D+-%3E%223%22
Quote: unJonQuote: ssho88Here is the integral solution:-
However, I think that series only converge if -1 < x < 1. So I think still not able to find length of arc 1/x from x = 1 to x = 3. Any comment?
link to original post
Just the same comment I made twice before.
https://www.wolframalpha.com/input?i=arc+length+1%2FX&assumption=%7B%22F%22%2C+%22ArcLength%22%2C+%22a%22%7D+-%3E%221%22&assumption=%7B%22F%22%2C+%22ArcLength%22%2C+%22b%22%7D+-%3E%223%22
link to original post
Thanks for your reply.
So Taylor series is not a viable way to find the arc length of 1/x ?
Quote: ssho88Quote: unJonQuote: ssho88Here is the integral solution:-
However, I think that series only converge if -1 < x < 1. So I think still not able to find length of arc 1/x from x = 1 to x = 3. Any comment?
link to original post
Just the same comment I made twice before.
https://www.wolframalpha.com/input?i=arc+length+1%2FX&assumption=%7B%22F%22%2C+%22ArcLength%22%2C+%22a%22%7D+-%3E%221%22&assumption=%7B%22F%22%2C+%22ArcLength%22%2C+%22b%22%7D+-%3E%223%22
link to original post
Thanks for your reply.
So Taylor series is not a viable way to find the arc length of 1/x ?
link to original post
I don’t know. Haven’t used Taylor series since college. Wolfram seems to think it’s a Puiseux type series.
https://www.wolframalpha.com/input?i=Taylor+%281+%2B+1%2Fx%5E4%29%5E0.5


