Royal Hunt

I saw two new video poker games at the Red Rock today. Royal Hunt was one of them. The other was Peek & Play, which I'll post about later in the week.

The game is based on the Triple-Play video poker. If the player pays an additional 15 credits, then he will enable the Royal Hunt feature. There, if the player gets two to four to a royal the game will spawn six extra hands that hold those cards to the royal. There is a different pay table for those extra hands.

Example:



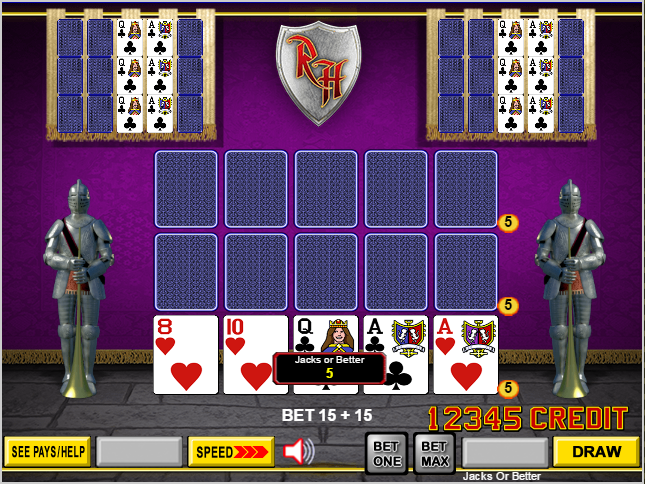
In the hand above, I got two to a royal, which automatically spawned the six extra hands. Click on any image for a larger version. Note that I could discard one of two to the royal, favoring the pair of queens, and I didn't have to sacrifice the feature. So, no strategy deviations.



Above is what happened after the draw.



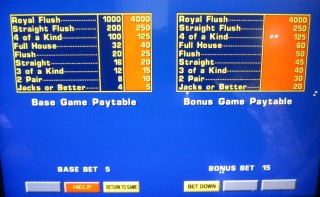
Above is just one pay table.

And finally some rule screens if the above wasn't clear.





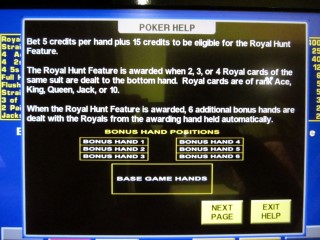
Note the rule about bonus hands 1-3 being evaluated first. The way I interpret the rules, if any royal cards are dealt to royal hand 1, then those cards will be cloned and also dealt to royal hand 4. Same with royal cards in hand 2 being duplicated to hand 5, and hand 3 to hand 6. I think this was to satisfy a Nevada gaming regulation that the probability of the highest award be greater than x. I'm always forgetting that value of x, but I'm sure MathExtremist can remind us.





The question for the poll is would you play Royal Hunt, given the same odds as conventional video poker?

To start the analysis, the following table shows the probability of getting 0 to 5 to a royal on the deal. In the situation of royals possible in multiple suits, the suit with the greatest number of royal cards is assumed.

Number to royal	Combinations	Probability
5	4	0.000002
4	940	0.000362
3	43,240	0.016637
2	622,200	0.239403
1	1,731,200	0.666113
0	201,376	0.077483
Total	2,598,960	1.000000

I've played this over a couple hours on videopoker. You're right about how the royals travel; top left maps to top right, middle left to middle right, etc. The paytable is nicely enhanced; once you trigger the extra hands, you usually make at least your total bet back. It's a reasonably fun game. Haven't seen a royal on it yet, though.

Assuming you mean "favoring the pair of kings"

In analyzing the game a question comes up is what cards would the game hold in the bonus hands if the player got this on the draw:

Jack of hearts
Queen of hearts
10 of clubs
Ace of clubs
Ace of spades

In this case there are 2 two-to-a-royals. The rules say the game picks one of them to hold -- but which one? The suited jack and queen are much better because there is a greater chance of forming straights, straight flushes, and high pairs.

Quote: Wizard

In this case there are 2 two-to-a-royals. The rules say the game picks one of them to hold -- but which one? The suited jack and queen are much better because there is a greater chance of forming straights, straight flushes, and high pairs.

I made a video poker game about 12 years ago that had a similar concept. It always chose the "royal cards" with the highest EV.

Quote: DRich

I made a video poker game about 12 years ago that had a similar concept. It always chose the "royal cards" with the highest EV.

Based on a very small sampling of this happening twice, Royal Hunt held the better cards both times. Of course, that could just be a 1 in 4 chance. This situation occurs once every 103 hands played.

I'd appreciate if other playing this at VideoPoker.com keep track of whether the game keeps the better or worse set of two cards when the player is dealt two sets of two to a royal in the same hand.




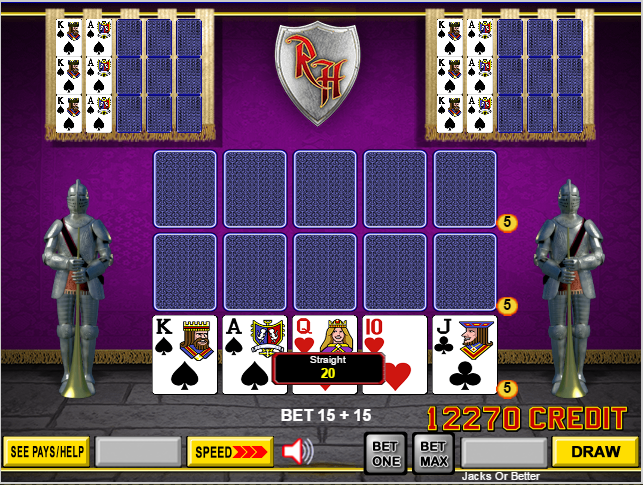
Oh, and I got a royal in waiting for these situations to occur:

In Nevada, it's a defacto 1 in 100 million. You can have events rarer than that in NV, but if you do, you have to put the exact odds on the payglass.

NJ and MS are an absolute 1 in 100M.

Most riverboat states are 1 in 50M (also the GLI recommendation)

CO (non-networked games) and CT are 1 in 17M, iirc.

These rules only apply to a single line though, so royal hunt should be fine anyway. There is a big rule change in Double STP thanks to these rules. And dealt royal with a deal multiplier automatically gets 20X...that's my dream hand. ;)

Quote: tringlomane

In Nevada, it's a defacto 1 in 100 million...

Thanks, good stuff. I retract what I wrote about the card cloning rule being because of this law. The game would likely be compliant without it.

My analysis without this rule shows a return of only about 83% for a pay table seen at the Red Rock, which was probably about 97% with it. Assuming the game will hold the better two to a royal, when two are dealt, and adding the card cloning rule, would make this a tricky analysis.

I can saw that the player will see 9.8 times as many royals per hand on the draw. The following table shows the probability of a royal in each hand, assuming 8-5 Jacks or Better in the base game.

Hand	Prob royal
Original	0.000024894
Bonus hand 1	0.000037850
Bonus hand 2	0.000185442
Total	0.000248186

Given that this game is based on Triple-Play, the player can expect to see one royal for every 1343.0761 hands on the deal.

Note: Updated 1-28-16

My guy at IGT just wrote to me saying that indeed Royal Hunt does choose the two to a royal with the higher expected value, when given the choice of two of them.

Royal Hunt is a fun game. Played it a good amount on VP.com when it first came out.

I showed it to a ploppy, he hit a royal, and tipped me $100. :) Well.....sort of!



Wizard, I forget if this is the game or not -- but, it only counts with 2, 3, or 4 to a RF, right? So if you get a dealt RF, you don't get 9x royals (3 main hands plus 1-3 and 4-6 bonus hands)?

card cloning rule question:
if you are dealt 4 to a royal, then those 4 cards are in bonus hands 1-3.
if any of those hands get the fifth card to make a royal, then the corresponding bonus hand on the right side automatically gets the royal as well?

and did IGT give out the payback table?

Quote: RS

Wizard, I forget if this is the game or not -- but, it only counts with 2, 3, or 4 to a RF, right? So if you get a dealt RF, you don't get 9x royals (3 main hands plus 1-3 and 4-6 bonus hands)?

Right, 2 to 4 only. No bonus hands on a dealt royal.

Quote: 100xOdds

card cloning rule question:
if you are dealt 4 to a royal, then those 4 cards are in bonus hands 1-3.
if any of those hands get the fifth card to make a royal, then the corresponding bonus hand on the right side automatically gets the royal as well?

Yes.

Quote:

and did IGT give out the payback table?

No yet. My contact there said Wednesday.

Since you have the IGT verification, you probably don't need the validation, but it has been my experience the game holds the higher RF EV cards consistently.

Interesting question about the Royal transfer if it happens in hands 1-3. I'm guessing not, but will be interested to hear. Since you'd get 3x royals on a dealt royal, it doesn't seem out of the question that a royal could transfer above.

Having a case of deja vu here. The animation and sounds with the suits of armor looks familiar like I played a game like this many years ago. Anyone else think that part of the game looks familiar?

Please have a gander at my new page of Royal Hunt Poker.

As always, I welcome comments, questions, and especially corrections.

Wizard, I must be missing something obvious but I don't see why this would be a difficult game to analyze. I am assuming that each bonus hand has all cards available and none were excluded based on the previous hands.

I may try to do this one myself and I am sure at that point I will probably understand better and draw the same conclusion that you did.

Quote: DRich

Wizard, I must be missing something obvious but I don't see why this would be a difficult game to analyze. I am assuming that each bonus hand has all cards available and none were excluded based on the previous hands.

It is difficult because there are lots of combinations for the non-royal cards removed from the Bonus hands. Add to that the inter-play between the left and right Bonus hands. It is doable but I deemed it not a worthwhile use of my time and the work would likely never be helpful with any other games.

Quote: Wizard

It is difficult because there are lots of combinations for the non-royal cards removed from the Bonus hands. Add to that the inter-play between the left and right Bonus hands. It is doable but I deemed it not a worthwhile use of my time and the work would likely never be helpful with any other games.

Thank you, I see it now. I didn't realize the initial five dealt cards were removed from the bonus hands. In your first example I saw the eight of spades in the base hand and the bonus hands. I thought that eight was dealt before the draw but now I realize it was a draw card. I knew I must have been missing something obvious.

Royal Hunt's a fun game. I've hit 2 or 3 royals on it playing live. I've hit another 3 maybe 4 RF's on VP.com. I wish you could turbo through the game, though, at least when you go into the bonus rounds. Seems like it takes an extra second or two to pay you after a bonus round. Really annoying.