Probability of non-event is therefore (99/100)
P(gap size zero) is therefore [ (99/100)^0 ] (1/100)
P(gap size one) is therefore [ (99/100)^1 ] (1/100)
P(gap size nineteen) is therefore [ (99/100)^19 ] (1/100)
Sum of all probabilities of gaps from zero to infinity is 1
Obtained by infinite series summation
(Edited 7:23 pm PST 03 Feb)
I was understanding the OP's question differently.Quote: pwcrabbProbability of event is (1/100)
Probability of non-event is therefore (99/100)
P(gap size one) is therefore [ (99/100)^1 ] (1/100)
P(gap size nineteen) is therefore [ (99/100)^19 ] (1/100)
Sum of all probabilities of gaps from zero to infinity is 1
Obtained by infinite series summation
link to original post
You say the P(1) = [ (99/100)^1 ] (1/100). This is the probability of one miss before a hit when you are starting at a hit.
In an infinite sequence, the hits come only once in 100 games. The probability of seeing a sequence of back to back hits starting at any particular game is 1 in 10,000. A sequence with two hits separated by exactly one miss appears with a probability 0.000099, etc.
Perhaps the OP can clarify which number he is seeking.
"how do I determine the chance of the gap between events happening?" leads me to believe it was my interpretation.Quote: BasilTheBorderIf there is an event occurring, say 1 in 100 times for ease of use, how do I determine the chance of the gap between events happening? So basically a "games since last event" counter. How many times would you expect it to occur on successive games? How many with exactly a 1 game gap? How many with exactly a 2 game gap ? How many with a 1000 game gap? etc., I'm thinking an infinite number of samples, rather than a small set. Is there a statistical formula to use? Any ideas very much welcomed.
link to original post
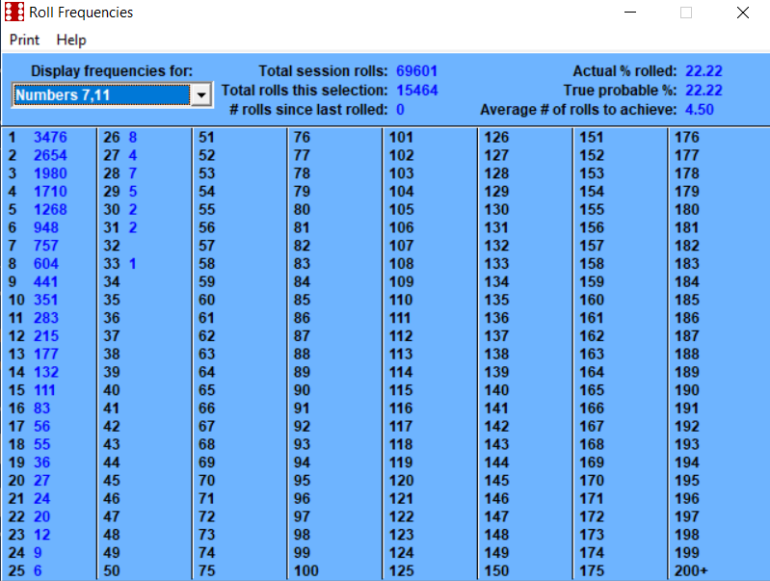
By pure coincidence there's a similar discussion using craps dice asking how often would it take to throw a "2" (1-1) and then mentions other totals including a "Natural Winnerl" (7 or 11). The enclosed picture (I hope ChumpChange doesn't mind me copying it here) shows how the frequencies decrease. In this case there are 8 ways out of 36 to throw a "Natural Winner". I've since replied by comparing this to an example of a long road where some of the buildings are pubs and the rest private houses, asking how far is it to the next pub. https://wizardofvegas.com/forum/gambling/craps/37930-roll-frequencies-after-69-6k-rolls-on-wincraps/#post880610
Quote: ChumpChange
OP specifically asked about "gap between events" but maybe OP meant gaps before the first event. These two are certainly not the same question.Quote: charliepatrickIf you start out afresh and ask what are the chances of an event with pr=1/100 happening on the 1st, 2nd etc. attempt; then the answer is 1st = 1/100, 2nd = 99/100 * 1/100 etc. This gives a distribution of "gaps" which just gradually decreases as the gap gets larger.
Basil, are you analyzing for:
1. The probability of first success on exactly a specific future trial?
2. The cumulative probability of first success on or before a specific future trial?
3. The expected number of gaps, or consecutive failures, of a certain size within a large universe of experiments?
4. The expected size of the next gap?
5. The mean size of all gaps?
6. Something else?
For gap sizes (n) from zero to any sufficiently large number to be illustrative, perhaps 500K, do the following:
1. Plot [ (99/100)^(n) ] [ (1/100) ]
This graph will be a gently sloped monotonic curve from (1/100) down towards the x axis asymptotically. It will remind you of Poisson.
2. Plot the incremental summation of the above series of terms. This graph will be a gently sloped monotonic curve from (1/100) up towards 1.0 asymptotically. Observe the value of (n) at which the curve exceeds 0.5, which means that likelihood has been achieved.
Please forgive yourself for any predilection for bell curve distributions. All of us have been conditioned to expect them everywhere.
I confess that I had the thought of the most probable gap being near 1/p for a second. The most probable gap has to be at 0 for the same reason that the most probable regular interval to see the first radioactive decay event is the first period. There are fewer nuclei after the first period ends.Quote: BasilTheBorderWhat I am interested in is the profile of gaps between successful events. Disregarding the lead up to the initial event, I think Mental's explanation fits my scenario. I have a slot game in development with a random event occurring 1 in 100 games. Logging the gaps between events gives a similar shaped curve to using Mentals approach. For some reason I was expecting a bell shaped curve centered around the 100 game gap. I need to brush up on my statistical knowledge! So in answer to your question, 6, or possibly 3. The profile of gaps between successful events.
link to original post
An easier way to think about it is that after every hit, the probability of a gap of length zero,1,2,... is the same as the question pwcrabb answered. The function you seek is pwcrabb'c function divided by p. If p=1, then P(0) =1 and and P(x!=1)=0.
The answer only works for an infinite series. The answer is only approximate for a finite series if you add any initial partial gap to any ending partial gap. You can check this by counting the number strings of (wrapped) consecutive zeros in a sequence of binary digits 0-(2^n). If n=3, 000 001 010 011 100 101 110 111. p=0.5,
P(3) = 1/(8*3)
P(2) = 3/(8*3)
P(1) = 3(8*3)
P(0) = 6/(8*3)
In your example there's a 10% chance of getting the feature retriggered within 11 spins, etc.
| Chance | Spins |
|---|---|
10% | 11 |
20% | 23 |
30% | 36 |
40% | 51 |
50% | 69 |
60% | 92 |
70% | 120 |
80% | 161 |
90% | 230 |
95% | 299 |
98% | 390 |
99% | 459 |
99.5% | 528 |
99.8% | 619 |
99.9% | 688 |
99.99% | 917 |
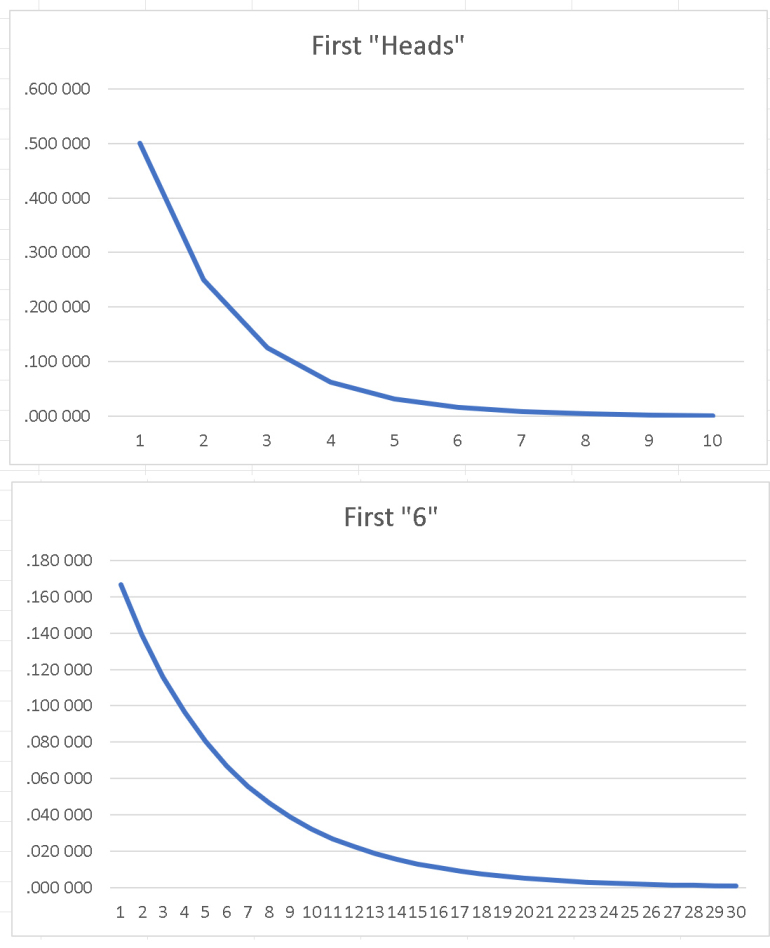
Thank You also for your report of results for the original problem for which P(success) is (1/100). Please notice especially that the cumulative probability reacbes 50% when (n) is 69, which seems correct at first glance. This would be the Median of the distribution.
Quote: Ace2Another way to get the median of 69 is ln(2) * 100, rounded to nearest integer
link to original post
Here is an approximation I get:
Let p be the probability of a particular trial being successful, and c the probability of being successful in n or fewer trials
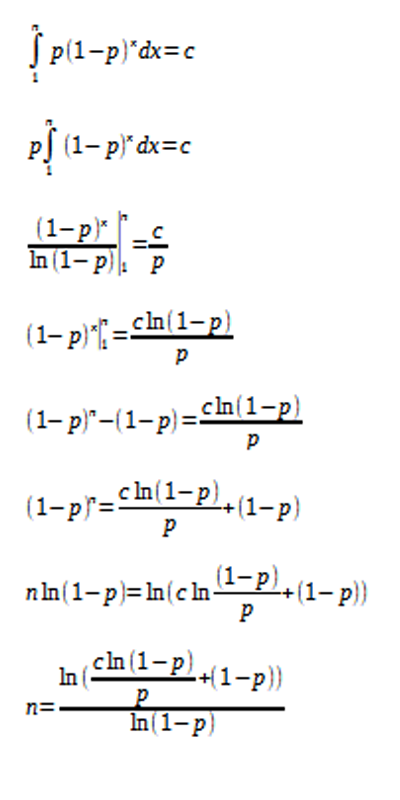
For p = 1/100 and c = 1/2, n = 71.49
I realize success canít actually happen in less than one trial, but the integral is for continuous time, not individual trialsÖwhich isnít the actual case either. Itís an approximation
Incidentally, Iíve found that integrals of Poisson processes give the correct answer only when integrating over all time (zero to infinity)
Monte Carlo simulations are useful for corroborating precise analytical answers. I have read of several gritty practitioners who swear by simulations as close enough for their non-engineering work.