Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
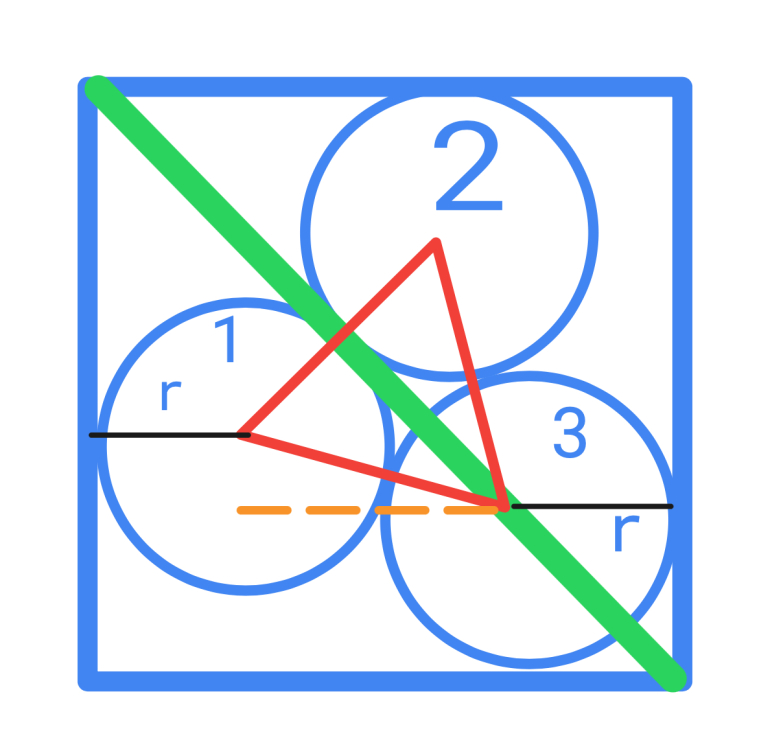
Quote: WizardWhat is the limit as x approaches 0, of ln(1-x)/sin(x)?
link to original post
Apply L'Hopital's Rule:
d/dx of ln (1-x) = -1 / (1-x)
d/dx of sin x = cos x
The answer is the limit as x approaches 0 of -1 / ((1 - x) cos x) = -1
Quote: ThatDonGuy
Apply L'Hopital's Rule:
d/dx of ln (1-x) = -1 / (1-x)
d/dx of sin x = cos x
The answer is the limit as x approaches 0 of -1 / ((1 - x) cos x) = -1
link to original post
I agree!
L'Hopital's Rule would have been an applicable rule in the Mean Girls calculus competition.
Direct: https://www.youtube.com/watch?v=oDAKKQuBtDo
Quote: WizardQuote: ThatDonGuy
Apply L'Hopital's Rule:
d/dx of ln (1-x) = -1 / (1-x)
d/dx of sin x = cos x
The answer is the limit as x approaches 0 of -1 / ((1 - x) cos x) = -1
link to original post
I agree!
L'Hopital's Rule would have been an applicable rule in the Mean Girls calculus competition.
Direct: https://www.youtube.com/watch?v=oDAKKQuBtDo
link to original post
Wiz,
Speaking of L'Hopital, (or more correctly, L'Hôpital), how would you like to have the "correct" spelling of your name changed retroactively?
Back when I took calculus, we spelled his name "L'Hospital" (which is how he himself spelled his name) and generally referred to him jokingly as "the Hospital guy".

According to Wikipedia:
"In the 17th and 18th centuries, the name was commonly spelled "l'Hospital", and he himself spelled his name that way. Since then, French spellings have changed: the silent 's' has been removed and replaced with a circumflex over the preceding vowel."
This whole "change the spelling" business reminds me of an old Dolton Edwards science fiction short story, "Meihem in ce Klasrum": read it here.
Dog Hand
Quote: DogHandWiz,
Speaking of L'Hopital, (or more correctly, L'Hôpital), how would you like to have the "correct" spelling of your name changed retroactively?
Back when I took calculus, we spelled his name "L'Hospital" (which is how he himself spelled his name) and generally referred to him jokingly as "the Hospital guy".
According to Wikipedia:
"In the 17th and 18th centuries, the name was commonly spelled "l'Hospital", and he himself spelled his name that way. Since then, French spellings have changed: the silent 's' has been removed and replaced with a circumflex over the preceding vowel."
This whole "change the spelling" business reminds me of an old Dolton Edwards science fiction short story, "Meihem in ce Klasrum": read it here.
Dog Hand
link to original post
Nobody has ever asked me that before. I think I favor changing the spelling to conform with the way language changes.
If 1000 people play the game each day, find the state lottery expected gain and describe its distribution?
Let S denote the state lottery total gain in 100 days, assuming that 1000 people play on each day.
Find ν:= E(S) and a value of c for which P {ν − c < S ≤ ν + c} ≈ .95
The player's expected gain on a $1 ticket is exactly -$0.50. (That's 0.001 * 499.00 + 0.999 * (-1.00).)
If 1000 people play the lottery each day, the state lottery's expected gain is 1000 * $0.50 = $500 per day. If the people select their numbers randomly (or if the lottery assigns the numbers randomly), the distribution of the lottery's gain per day is a binomial distribution with a standard deviation of 500 * sqrt(1000 * 0.001 * 0.999) ≈ $499.75.
S, the lottery's total gain in 100 days at 1000 tickets per day, would have the same distribution as selling 100,000 tickets. The distribution for S would be a binomial distribution with a standard deviation of 500 * sqrt(100,000 * 0.001 * 0.999) ≈ $4,997.50.
To find the value of c, I would use a normal distribution with mean of $50,000 and standard deviation of $4,997.50. I find that c is about 1.96 * $4,997.50 ≈ $9,795.
Edit: S would have to be a multiple of $500, so a better distribution to use would be Poisson's. I find that with c = 19 * $5,000 = $9,500, Poisson's distribution gives P {ν − c < S ≤ ν + c} = 94.9%.
Another edit: Better yet, we can use the binomial distribution directly with n = trials = 100*1000 and p = probability of success = 1 / 1000 to get c = $9,500. The probability of having fewer than 120 winners but more 80 is 94.9% as in the Poisson result.
(I welcome any corrections to my answers.)
Answers: −$0.50; 500; 1000 − 500X, where X ∼ Poisson(λ = 1)
Since
P {v - c < S <= v + c} = P{|S - v| / 5000 <= 5000 }
and the upper 0.025 quantile of N(0,1) is about 1.96, we have
c/5000 = 1.96 which is c=9800
Quote: chevy
I think it does have to be with the three circles symmetric about the diagonal.
Start with two circles stacked on top (e.g. 2&3 in my pic) - need square of height 4r=4*1=4
then rotate the three circle arrangement counterclockwise, the height gets smaller
Eventually when you cross the diagonal the width starts to get wider until the case where two circles are side by side (1&3 in my pic).....so square is 4r = 4 wide.
That is process is symmetric, so the midpoint is the min.....(unless it hits a min, increases to the diagonal, then back to a min, before increasing to the max).....Handwaving says it isn't.
Then
Green diagonal at 45 degrees above horizontal
red equilateral triangle connecting centers has side 2r = 2 and lower side is at 30 degrees below green. Or 15 degrees above orange dashed line
Orange dashed line is (red side) * cos(15) = 2 cos(15)
half angle formula....
cos(15)= sqrt((1+cos(30))/2) = sqrt ( (1+ sqrt(3)/2)/2) = sqrt((2+sqrt(3))/4) = sqrt(2+sqrt(3)) / 2
So orange dashed = sqrt(2+sqrt(3))
and width of square is
black + orange dashed + black
1+sqrt(2+sqrt(3))+1
2+sqrt(2+sqrt(3)) or about 3.93185165258
PS: I am embarrassed just how sloppy this is, but a it is an attempt
link to original post
I finally got back to this one and agree. Very clever solution. Mine was much more complicated and error prone.
Here is my solution (PDF), which is the same as Chevy's. Note that I express is without the cosine function.
Quote: WizardQuote: chevy
I think it does have to be with the three circles symmetric about the diagonal.
Start with two circles stacked on top (e.g. 2&3 in my pic) - need square of height 4r=4*1=4
then rotate the three circle arrangement counterclockwise, the height gets smaller
Eventually when you cross the diagonal the width starts to get wider until the case where two circles are side by side (1&3 in my pic).....so square is 4r = 4 wide.
That is process is symmetric, so the midpoint is the min.....(unless it hits a min, increases to the diagonal, then back to a min, before increasing to the max).....Handwaving says it isn't.
Then
Green diagonal at 45 degrees above horizontal
red equilateral triangle connecting centers has side 2r = 2 and lower side is at 30 degrees below green. Or 15 degrees above orange dashed line
Orange dashed line is (red side) * cos(15) = 2 cos(15)
half angle formula....
cos(15)= sqrt((1+cos(30))/2) = sqrt ( (1+ sqrt(3)/2)/2) = sqrt((2+sqrt(3))/4) = sqrt(2+sqrt(3)) / 2
So orange dashed = sqrt(2+sqrt(3))
and width of square is
black + orange dashed + black
1+sqrt(2+sqrt(3))+1
2+sqrt(2+sqrt(3)) or about 3.93185165258
PS: I am embarrassed just how sloppy this is, but a it is an attempt
link to original post
I finally got back to this one and agree. Very clever solution. Mine was much more complicated and error prone.
Here is my solution (PDF), which is the same as Chevy's. Note that I express is without the cosine function.
link to original post
That means
mine =?= yours
sqrt(2+sqrt(3)) = (sqrt(6) + sqrt(2))/2
2+sqrt(3) = (6 + 2sqrt(12) + 2)/4
2+sqrt(3) = (8 + 4sqrt(3))/4
2+sqrt(3) = 2+sqrt(3)
YEP, checks out.....though I don't see a simplification I remember from algebra that converts one to the other.
Let fX,Y(x,y) be the joint PDF of two random variables X and Y, defined as follows:
fX,Y(x,y) = {cxy^2 for 0< x < 1 and 0< y < 2
{0 otherwise
Find the constant c such that fX,Y(x,y) is a valid joint PDF.
Then, compute the marginal PDFs of X and Y, denoted as fX(x) and fY(y), respectively.
Finally, compute P(X < 0.5 and Y > 1).


Presenting a plethora of pi perplexities...
:strip_icc()/pic8091195.png)
Pictured above are three identical boxes packed with pies.
Which box contains the most pie?
Assume all pies are the same height.

You have a pizza with crust thickness 'a' and radius 'z'.
What's the volume of the pizza?
Assume a perfect, flat circle.
:strip_icc()/pic8091194.png)
P = ?
I = ?
E= ?
Riddle me this Rebus riddle.
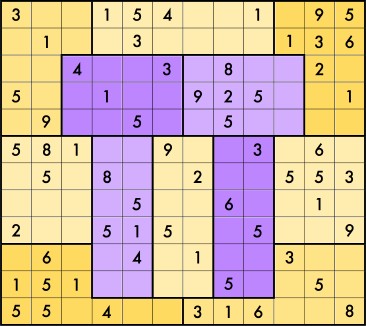
For those of you with some time on this Pi Day, try solving this sudoku. The rules are the same as regular sudoku except...
--The grid is 12x12.
--Each row, column, and colored block contains the first 12 digits of pi
3 1 4 1 5 9 2 6 5 3 5 8
in some order. In particular, there are two 1s, one 2, two 3s, one 4, three 5s, one 6, no 7s one 8, and one 9.
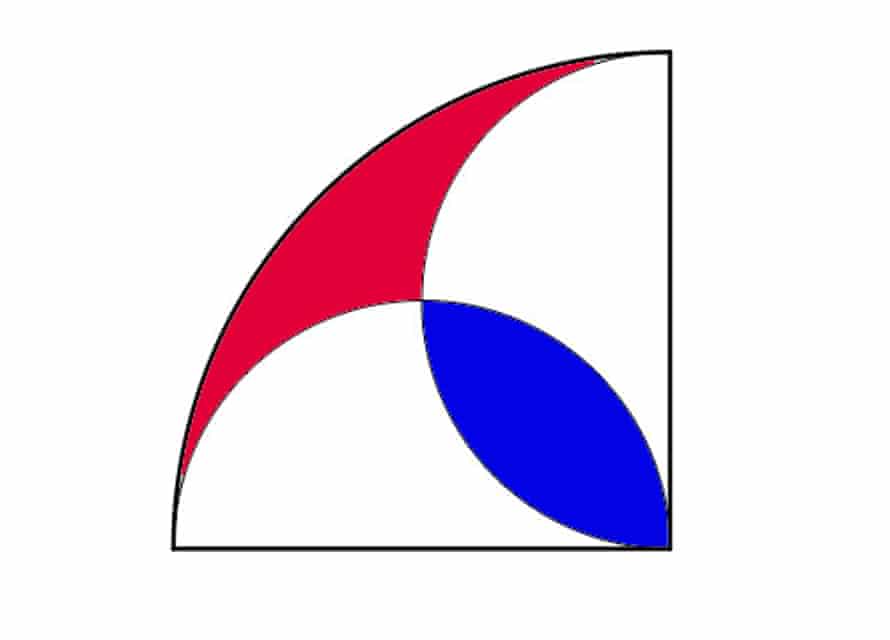
Illustrated above is a quarter-circle, containing two semicircles of smaller circles.
Prove that the red segment has the same area as the blue.


all the same
if D is side of box
(pi/4) D^2 = 4 * (pi/4) (D/2)^2 = 16 * (pi/4) (D/4)^2
pizza volume = pizza
PIE = 169
sqrt(16) + 9 = 4+9 = 13 = sqrt(169)
?? pi-rate = pirate ??
Call the side of the big quarter circle = r
Area of quarter circle = (1/4) pi * r^2
Area of small semicircle = (1/2) pi (r/2)^2 = (1/8) pi * r^2
Then (area of quarter circle = { 2 * area of semicircle - BlueArea } + RedArea ...... (blue is counted twice in semicircles, so take one out)
(1/4) pi * r^2 = {2 * (1/8) pi * r^2 - BlueArea } + RedArea
0= - BlueArea + RedArea
BlueArea=RedArea
Quote: chevypicking the low hanging fruit
all the same
if D is side of box
(pi/4) D^2 = 4 * (pi/4) (D/2)^2 = 16 * (pi/4) (D/4)^2
pizza volume = pizza
PIE = 169
sqrt(16) + 9 = 4+9 = 13 = sqrt(169)
?? pi-rate = pirate ??
Call the side of the big quarter circle = r
Area of quarter circle = (1/4) pi * r^2
Area of small semicircle = (1/2) pi (r/2)^2 = (1/8) pi * r^2
Then (area of quarter circle = { 2 * area of semicircle - BlueArea } + RedArea ...... (blue is counted twice in semicircles, so take one out)
(1/4) pi * r^2 = {2 * (1/8) pi * r^2 - BlueArea } + RedArea
0= - BlueArea + RedArea
BlueArea=RedArea
link to original post
Correct!
Well done.
---------------------------------------------
Quote: GialmereQuote: chevypicking the low hanging fruit
all the same
if D is side of box
(pi/4) D^2 = 4 * (pi/4) (D/2)^2 = 16 * (pi/4) (D/4)^2
pizza volume = pizza
PIE = 169
sqrt(16) + 9 = 4+9 = 13 = sqrt(169)
?? pi-rate = pirate ??
Call the side of the big quarter circle = r
Area of quarter circle = (1/4) pi * r^2
Area of small semicircle = (1/2) pi (r/2)^2 = (1/8) pi * r^2
Then (area of quarter circle = { 2 * area of semicircle - BlueArea } + RedArea ...... (blue is counted twice in semicircles, so take one out)
(1/4) pi * r^2 = {2 * (1/8) pi * r^2 - BlueArea } + RedArea
0= - BlueArea + RedArea
BlueArea=RedArea
link to original post
Correct!
Well done.
---------------------------------------------...it would never end.BackwardsCake
link to original post
Love Chuck Jokes
Chuck doesn't do push ups, he pushes the earth down
He can judge a book by its cover
He doesn't sleep, he waits
When he jumps in the water, he doesn't get wet, the water gets Chuck Norris
Chuck counted to infinity, twice
Chuck can divide by zero

That was fun!
Dog Hand
Quote: DogHandPi-Doku Answer
That was fun!
Dog Hand
link to original post
Correct!!
Well done. (As a bonus, you have now memorized the first 12 digits of pi. Watch the girls in the math club swoon.)
Consider Dog Hand's response to be official.
------------------------------------------
There are N people in a room. For any pair of people in the room, the two of them are either friends with each other or not. Friendship is always reciprocal and people cannot be friends with themselves. Prove there are at least two people in the room who have the same number of room-friends.
When N=n, we assume there are at least 2m people who have the same number, x, of room-friends.
By math deduction, when N=n+1, ….
Quote: rackuunI don't know if this one was posted before:
There are N people in a room. For any pair of people in the room, the two of them are either friends with each other or not. Friendship is always reciprocal and people cannot be friends with themselves. Prove there are at least two people in the room who have the same number of room-friends.
link to original post
Assume that each person has a different number of friends.
This is possible only if one has no friends, one has 1 friend, one has 2 friends, and so on, with the last one having N-1 friends.
This means the person with N-1 friends is friends with everyone else in the room, which is impossible as the person with no friends is not friends with this person.
Therefore, the assumption that each person has a different number of friends is false.
Quote: ThatDonGuyQuote: rackuunI don't know if this one was posted before:
There are N people in a room. For any pair of people in the room, the two of them are either friends with each other or not. Friendship is always reciprocal and people cannot be friends with themselves. Prove there are at least two people in the room who have the same number of room-friends.
link to original post
Assume that each person has a different number of friends.
This is possible only if one has no friends, one has 1 friend, one has 2 friends, and so on, with the last one having N-1 friends.
This means the person with N-1 friends is friends with everyone else in the room, which is impossible as the person with no friends is not friends with this person.
Therefore, the assumption that each person has a different number of friends is false.
link to original post
👍 Nice
If N=2 and they are not friends, is this true that there are at least two people who have the same number, 0, of room-friends?
234.8326629288898
Integrate from 0 to infinity of 1-(1-exp(-x/38)*(1+x/38))^38 dx
Recommended integral calculator: https://www.integral-calculator.com/
Quote: WizardThe question was asked in this post on the average number of spins to see every number appear at least twice in double-zero roulette?
234.8326629288898
Integrate from 0 to infinity of 1-(1-exp(-x/38)*(1+x/38))^38 dx
Recommended integral calculator: https://www.integral-calculator.com/
link to original post
The exact answer, calculated through a Markov chain process, is
2,458,532,792
,431,545,299,268,331,086,172,570,342,312,718,399,986,188,067
,613,993,736,050,899,703,294,263,621,414,373,376,335,532,123
,938,814,367,114,586,068,064,224,623,137,338,487,255,215,140
,008,621,838,160,580,491,305,106,138,247,464,350,795,459,486
,531,836,562,054,491,448,024,234,478,387,675,642,506,165,051
,266,071,873,671,771,900,922,226,332,086,888,171,157,513,993
,773,263,459,648,019,582,058,157,468,484,735,864,723,796,556
,010,777,275,053,180,121,803,203,922,520,306,071,448,436,764
,103,411,971,842,531,832,013,580,185,101,482,792,146,107,877
,371,534,984,353,278,390,414,808,452,594,198,307,228,367,261
over 10,469,296
,569,600,366,313,766,776,904,675,214,787,660,719,539,249,122
,838,110,753,732,469,863,621,352,350,201,672,413,287,522,823
,017,184,089,776,680,121,455,346,561,472,842,277,765,179,834
,313,091,454,122,181,241,307,952,873,173,734,004,633,490,787
,983,474,048,654,417,920,804,096,222,705,207,398,226,915,954
,866,956,131,936,567,944,994,893,548,485,765,436,847,000,729
,947,022,400,734,253,517,093,794,023,492,037,172,521,077,848
,152,918,335,557,895,072,383,721,878,928,916,078,101,947,708
,069,094,178,209,223,588,432,334,788,347,805,884,617,850,880
,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
which is about 234.83266292891, although I am not sure how many decimal places of accuracy Visual C# floating point division has

For these variations, it's the 70s and you love watching "Let's Make A Deal." In fact, you watch it so much you begin to notice things.
Eventually you become a contestant on the show and confront the three doors yourself. You pick door #1. Monty then walks to door #2 and opens it to reveal a goat.
What is the probability that switching to door #3 wins?
On the other hand, he sometimes gives false tells—i.e., arches his left eyebrow in this way when a contestant has chosen a goat door. He does this 10% of the time a goat door is chosen.
Now, you're on the show and have selected a door. You then see Monty's left eyebrow arch three times after he opens another door to reveal a goat. He asks if you wish to switch doors.
What is the probability you'll win the car if you don't switch and stick with your initial door choice?
Quote: WizardWaiting to get graded...
link to original post
If he is waiting to get more answers, here are mine:
The probability that door 3 is shown if door 1 has the prize is 1/4
The probability that door 3 is shown if door 2 has the prize is 1
The probability that door 3 is shown if door 3 has the prize is 0
The probability of winning by switching = (1/4) / (1 + 1/4 + 0) = 1 / 5
The probability that Monty twitches if the prize is selected is 19/20
The probability that Monty twitches if a goat is selected is 1/10
The probability of winning by not switching = (19/20) / (19/20 + 1/10) = 19 / 21
Quote: ThatDonGuy
If he is waiting to get more answers, here are mine:
link to original post
I see we have a small difference on Monty's Tell. Of course, I could easily be the one in error.

So far, the Wizard is correct about Monty's Tell.
Lazy Monty, however, remains unsolved.
Quote: GialmereApologies for my tardiness. This holiday weekend has gotten much busier than anticipated.
So far, the Wizard is correct about Monty's Tell.
Lazy Monty, however, remains unsolved.
link to original post
In that case I’ll try:
In that case now that I have picked door #1, Monty chooses door 2 one-third of the time when the car is in door #3 and one-third times three-quarters of the time when the car is in door #1.
So 1/3 * 3/4 / (1/3 + 1/3 * 3/4) = 3/7 chance that door #1 has the car.
Better off switching to win 4/7 of the time.
Quote: ThatDonGuyQuote: WizardWaiting to get graded...
link to original post
If he is waiting to get more answers, here are mine:
The probability that door 3 is shown if door 1 has the prize is 1/4
The probability that door 3 is shown if door 2 has the prize is 1
The probability that door 3 is shown if door 3 has the prize is 0
The probability of winning by switching = (1/4) / (1 + 1/4 + 0) = 1 / 5
link to original post
...that Monty opens door 2.
The probability that door 2 is shown if door 1 has the prize is 3/4
The probability that door 2 is shown if door 2 has the prize is 0
The probability that door 2 is shown if door 3 has the prize is 1
The probability of winning by switching = 1 / (3/4 + 0 + 1) = 4 / 7
Quote: WizardPr(win if you don't switch)=19/23
link to original post
Quote: unJonI read the assumption as saying if the contestant picks door #1 and the car is behind door #1, so Monty is free to choose to open either door 2 or 3, then 75% of the time he chooses door 2.
In that case now that I have picked door #1, Monty chooses door 2 one-third of the time when the car is in door #3 and one-third times three-quarters of the time when the car is in door #1.
So 1/3 * 3/4 / (1/3 + 1/3 * 3/4) = 3/7 chance that door #1 has the car.
Better off switching to win 4/7 of the time.
link to original post
Quote: ThatDonGuy
...that Monty opens door 2.
The probability that door 2 is shown if door 1 has the prize is 3/4
The probability that door 2 is shown if door 2 has the prize is 0
The probability that door 2 is shown if door 3 has the prize is 1
The probability of winning by switching = 1 / (3/4 + 0 + 1) = 4 / 7
link to original post
Correct!!
Good show.


Or consider an extreme case. Suppose that lazy Monty is so lazy that, after you pick door #1, he will always show you a goat behind door #2 ... unless he can't. If he shows you a goat behind door #3, you know with 100% certainty that the car is behind door #2.
--------------------------------------

There sits before you a standard, well-shuffled deck of 52 playing cards. I remove a card and look at it without showing it to you. I set the card aside and truthfully inform you that it is not the A♦. I point back at the deck and tell you to draw a card.
What, from your perspective, is the probability of drawing the 9♣?
Quote: Gialmere
There sits before you a standard, well-shuffled deck of 52 playing cards. I remove a card and look at it without showing it to you. I set the card aside and truthfully inform you that it is not the A♦. I point back at the deck and tell you to draw a card.
What, from your perspective, is the probability of drawing the 9♣?
link to original post
Assuming you intended to check if the first card was the A♦ before you looked at it, I get a probability of 50 / 512 of my drawing the 9♣.
Quote: GialmereThere sits before you a standard, well-shuffled deck of 52 playing cards. I remove a card and look at it without showing it to you. I set the card aside and truthfully inform you that it is not the A♦. I point back at the deck and tell you to draw a card.
What, from your perspective, is the probability of drawing the 9♣?
link to original post
Knowing nothing else about your statement (e.g. would you have said "It is the Ace of Diamonds" if it was), this sounds like a variation on the Monty Hall problem; I think the answer is 1/52.
Quote: ChesterDog
Assuming you intended to check if the first card was the A♦ before you looked at it, I get a probability of 50 / 512 of my drawing the 9♣.
link to original post
Correct!
Well done.
---------------------------------
And yes, it's as easy as you'd think.