Poll
 | 5 votes (26.31%) | ||
 | 2 votes (10.52%) | ||
 | 1 vote (5.26%) | ||
 | 3 votes (15.78%) | ||
 | 7 votes (36.84%) | ||
 | 4 votes (21.05%) | ||
 | 2 votes (10.52%) | ||
 | 5 votes (26.31%) | ||
 | 2 votes (10.52%) | ||
 | 4 votes (21.05%) |
19 members have voted
This is a tough one, so I'll give some hints.
The equation of a dangling rope from two points at the same height is a catenary.
The general equation of a catenary is a*cosh(x/a) - a = a * (exp(x/a)-exp(-x/a))/2 - a.
I'll give you these derivatives:
cosh'(x) = sinh(x)
sinh'(x) = cosh(x)
And finally this one nobody should be without:
cosh^2(x) - sinh^2(x) = 1
That should be enough to get you to the answer.
As usual, please put answers in spoiler tags and not too much cheating.
Don, I'd kindly ask you to give the rest of the forum 24 hours to earn a beer this time.
The question for the forum is what is the answer?
Is the answer different on the moon? (gravitational force = 1/6-th that of Earth).
I don't have time to scrape the rust off what I remember about solving differential equations, but I'll take a guess at the bonus question.Quote: teliotI hope you don't mind a bonus question Mike --
Is the answer different on the moon? (gravitational force = 1/6-th that of Earth).
When was the last time you used that in casual conversation?
Quote: teliotI hope you don't mind a bonus question Mike --
Is the answer different on the moon? (gravitational force = 1/6-th that of Earth).
I actually have wondered this for about 40 years. Since a catenary (why doesn't my spell checker like that word?) is noteworthy because there is equal gravitational force at every point, if that is the correct way of putting it, I would say it is the same on the moon.
Quote: OnceDearI can't remember how to do the maths. But I do remember that the curve is called a 'catenary'
When was the last time you used that in casual conversation?
I look for any excuse to steer conversations towards such topics. Probably explains, in part, why I can never hold a woman's attention for more than a minute.
Quote: WizardI actually have wondered this for about 40 years. Since a catenary (why doesn't my spell checker like that word?) is noteworthy because there is equal gravitational force at every point, if that is the correct way of putting it, I would say it is the same on the moon.
Well itís been more than 20 years since we derived the catenary in Calc 3 in college, but I thought it wasnít just equal gravitational force but also that being equal to the force caused by the tension of the rope. If thatís right, then less gravity means the balance would be with less rope tension, meaning the y-axis minimum would be higher if gravity was less.
But I could have that totally wrong.

I think it could be said the shape of such arches work because the gravitational pressure is equally distributed along the curve. In other words, there is no weakest link.
p.s. You guys have just under 11 hours before Don swoops in and snatches another beer.
Quote: unJon...then less gravity means the balance would be with less rope tension...
Instead of thinking about the effect of the local value of g, we can ask, "Do both a string catenary and a heavy chain catenary of the same length take the same shape?"
Gender 'X': New York City to add third gender option to birth certificates
I used to assign questions like this when I taught diff-eq, In my opinion, it's a bit advanced and not intrinsically interesting. Maybe that's the issue more than stumping folks. The one before this involved Riemann surfaces for the log function. Maybe you're missing your college days ...Quote: WizardI'm proud to say I have stumped the forum, apparently, except for Don, who may jump in in 3.5 hours.
I think source material from elementary number theory, geometry and recreational mathematics is more in the spirit of such questions.
For the line which is the rope, x=0 being the center...
y = a cosh (x/a)
y = 50
a = 10
So x = 22.924 which is the x coordinate of the right pole. The total distance between would be double that or 45,85.
That could also be approximated by:
Ln (50 / 10 * 2) * 10 * 2 = 46.05
Quote: teliotI think source material from elementary number theory, geometry and recreational mathematics is more in the spirit of such questions.
Sometimes I take pleasure in a problem that helps me dust off some long-forgotten skills.
Anyway, if you care to suggest the next problem, I'm sure the forum would be up to the challenge.
For a catenary, I think:
y = cosh (x/a)-a = 40
and the arc length is = sinh (x/a) which must equal 50 meters, half of the rope length.
so:
cosh(x/a) = (40/a)-a
sinh(x/a) = 50/a
Using Wizard's hint that cosh^2 (x/a) -sinh^2 (x/a) = 1
I get ((40+a)^2 )/a^2 - (50/a)^2=1
So a^2 = a^2 +40a+1600-2500
900= 40a
thus,
a=22.5
Thus sinh(x/22.5) = 50/22.5
so the half-distance between the poles, x = 22.5* arcsinh(50/22.5)
And the distance between the poles =2x= 45*arcsinh(50/22.5) which is approximately 69.2468 meters
Quote: gordonm888I just saw this a little while ago and I have struggled with this. Not sure this is the right answer.
It isn't what I get. Let's say there was a short pole 10 meters high directly between the poles. If the rope went from the left pole, directly to the top of the center pole and up to the right, wouldn't it's length be 2*((69.2468/2)^2 + 40^2)^0.5 = 105.9642 meters. We're given it is only 100 meters, so I don't think the poles could be that far apart.
You know, I enjoy reading old math books as well. Over the last few days I re-read "Elementary Number Theory" by Burton. My goal was was to remember the easy way to prove the "Four Square Theorem" using the Quaternions, but it didn't come back. Sigh ...Quote: WizardAnyway, if you care to suggest the next problem, I'm sure the forum would be up to the challenge.
This is actually a very easy read ...
http://www.mathcs.duq.edu/~haensch/411Materials/Quaternions.pdf
Quote: teliotYou know, I enjoy reading old math books as well. Over the last few days I re-read "Elementary Number Theory" by Burton. My goal was was to remember the easy way to prove the "Four Square Theorem" using the Quaternions, but it didn't come back. Sigh ...
This is actually a very easy read ...
http://www.mathcs.duq.edu/~haensch/411Materials/Quaternions.pdf
I think I regret I asked. That is beyond my level. Pass the dunce cap, I'll be sitting in the corner.
p.s. Are Quaternions those things programmers use for moving graphics? I hope Ahigh sees this.
No dunce cap for you!Quote: WizardI think I regret I asked. That is beyond my level. Pass the dunce cap, I'll be sitting in the corner.
p.s. Are Quaternions those things programmers use for moving graphics? I hope Ahigh sees this.
You know the Quaternions, i, j, k and such ... Diana said she used the Quaternions in one of the slots she programmed -- she was very proud of it. I never saw her actual implementation, but you know she had some tricks.
A long time ago I sent you a book, The Incredible Dr. Matrix. Maybe try and find that and re-read a bit of it? I would say it was one of the best math books ever. There are some wonderful tidbits in there that might inspire some questions.
Quote: WizardA 100 meter rope is suspended from the top of two 50-meter poles. The lowest point of the rope is 10 meters from the ground. How far apart are the poles?...
I tried to solve the problem with math, but eventually had to give up and learn the math from YouTube. It was fun, though--thanks for the problem!
Quote: ChesterDogI cut a piece of thread and taped its ends to the ceiling so that 100 cm of it were between the pieces of tape. Adjusting the tape so the thread hung down 40 cm, I found that the ends were about 50.5 cm apart. So, the answer to your question should be near 50 meters.
I tried to solve the problem with math, but eventually had to give up and learn the math from YouTube. It was fun, though--thanks for the problem!
Very good work there! I'm impressed. Your answer is indeed close. You certainly deserve some extra credit, but I'm still looking for an answer to at least six decimal places. Even I don't know an exact expression of the answer.
Don's 24-hour waiting period has lapsed so, Don, you're welcome to jump in and prove your dominance.
As long as CD has posted a close approximation, I'll post this graph I did what the curve looks like.
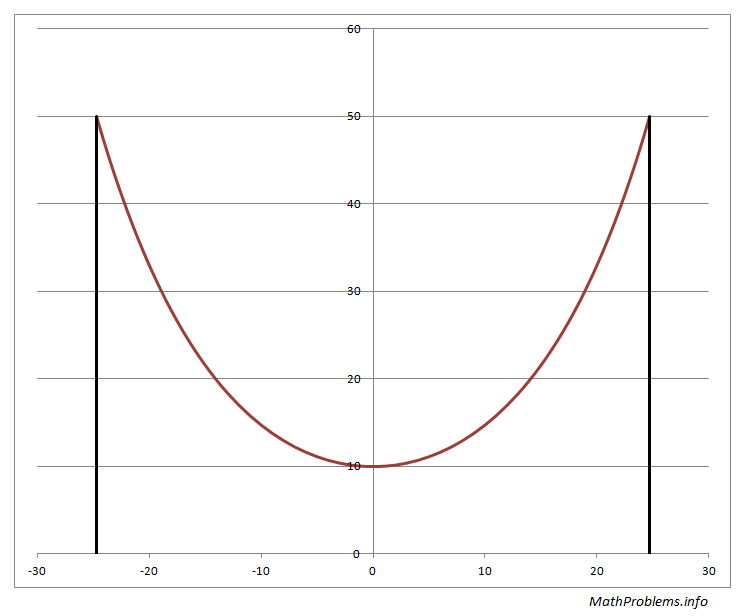
I get 49.437553.
I did need to re-learn some stuff, such as finding the length of a curve.
Using the basic formula, I want to find the distance from center, where the height of the curve is 50.
The basic formula is y = a*cosh(x/a)-a+10. For y=50, solve for x: x=a*cosh-1((40+a)/a)
The second part is to find the length of the curve. It's too hard to type here, but the length of the curve is
2*a*sinh(x/a) = 2*a*sinh(cosh-1((40+a)/a)) when plugging in the first formula.
Using this, we can solve for a, when the length = 100.
I just put this formula in excel and used Goal Seek to find a. Turns out a = 11.25 (I think exactly).
Then find the distance from the center to one pole: x=11.25*cosh-1((40+11.25)/11.25) = 24.7187765. The total distance between the two poles is 2*24.7187765 = 49.437533.
I also read that a = (horizontal force applied to rope)/(weight of rope). In this case, I will call the weight 100 and each end point supports 50 of that. The horizontal force = 50 * the sin of the angle at the end point = 50/(dy/dx(a*cosh(x/a)-a+10) = 50/(a*sinh(x/a)). This is the same formula that I found when I calculated the length of the curve.
Thanks, Mike. This was fun and it made me re-learn some things.
I agree with CrystalMath's 49.437553.
(45/2)*ArcSinh(40/9) = 49.437553
Quote: CrystalMath
I get 49.437553.
I did need to re-learn some stuff, such as finding the length of a curve.
Using the basic formula, I want to find the distance from center, where the height of the curve is 50.
The basic formula is y = a*cosh(x/a)-a+10. For y=50, solve for x: x=a*cosh-1((40+a)/a)
The second part is to find the length of the curve. It's too hard to type here, but the length of the curve is
2*a*sinh(x/a) = 2*a*sinh(cosh-1((40+a)/a)) when plugging in the first formula.
Using this, we can solve for a, when the length = 100.
I just put this formula in excel and used Goal Seek to find a. Turns out a = 11.25 (I think exactly).
Then find the distance from the center to one pole: x=11.25*cosh-1((40+11.25)/11.25) = 24.7187765. The total distance between the two poles is 2*24.7187765 = 49.437533.
I also read that a = (horizontal force applied to rope)/(weight of rope). In this case, I will call the weight 100 and each end point supports 50 of that. The horizontal force = 50 * the sin of the angle at the end point = 50/(dy/dx(a*cosh(x/a)-a+10) = 50/(a*sinh(x/a)). This is the same formula that I found when I calculated the length of the curve.
Thanks, Mike. This was fun and it made me re-learn some things.
I agree!!! Very good work there. You and both ChesterDog have both well earned a beer.
Good idea about putting the answer in the form of sinh^-1(x).
Looking up the equation for sinh^-1(x), I find an exact expression of the answer is (45/2) × ln〖( 40/9+ √(1+ 〖40/9〗^2 ))〗
Wiz full solution (PDF)
And it's amazing to me that your (45 ln(40/9+Ā(1+(40/9)2 )1/2))/2 simplifies to 45ln3.
Quote: ChesterDogThanks!
I did not know that sinh-1=ln[x+(1+x2)1/2].
And it's amazing to me that your (45 ln(40/9+Ā(1+(40/9)2 )1/2))/2 simplifies to 45ln3.
Good catch! I didn't know it simplified to that. Very elegant. For what it's worth, I chose the pole and rope length arbitrarily.
Quote: WizardQuote: ChesterDogThanks!
I did not know that sinh-1=ln[x+(1+x2)1/2].
And it's amazing to me that your (45 ln(40/9+Ā(1+(40/9)2 )1/2))/2 simplifies to 45ln3.
Good catch! I didn't know it simplified to that. Very elegant. For what it's worth, I chose the pole and rope length arbitrarily.
That is crazy. All the stuff inside the ln evaluates to 9, so we have 45*ln(9)/2, and ln(9)/2 = ln(3).
One step I struggle with in this whole problem is scaling a catenary. The general form is
y = a * cosh(x/a).
I can see how this scales the catenary, but would these curves be catenaries:?
y = cosh(x/a)
y = a*cosh(x)
Quote: unJonHaving now refreshed on the Wikipedia page, Iím confused. The ďaĒ in the catenary function appears to equal the Horizontal Force dividend by the mass per unit of length and the distance between poles. Is that correct, and if so, what assumptions about force and mass were used to derive a=11.25?
I looked at it more as a math problem. See my posted solution for how I arrived at the value for a.
Quote: WizardI forgot to congratulate you on looking at this more like a physics problem.
One step I struggle with in this whole problem is scaling a catenary. The general form is
y = a * cosh(x/a).
I can see how this scales the catenary, but would these curves be catenaries:?
y = cosh(x/a)
y = a*cosh(x)
According to http://xahlee.info/SpecialPlaneCurves_dir/Catenary_dir/catenary.html, "It is worthwhile to note that catenary has only one shape (it is not a family of curves)."
So, if the formula for a curve can be transformed into the general form of the catenary, y = a * cosh(x/a), by making these substitutions, Y = ky and X = kx, then it's a catenary, too. Note that the same scaling factor, k, must be used for both X and Y.
For example, is Y = coshX a catenary? Let Y=ky and X=kx. Then ky = cosh(kx). y = (1/k) cosh(kx). Set 1/k = a, then y = a cosh(x/a). So Y=coshX is a catenary.
Regarding Y = cosh(X/a), let Y=ky and X=kx. Then ky = cosh(kx/a). y = (1/k) cosh(kx/a). Let A = 1/k, then y = A cosh(x/(aA)). This is a catenary only if a=1, in which case the formula would be y = A cosh(x/A).
The same goes for y=a*cosh(x). It's a catenary only if a = 1.
Quote: ChesterDogSo, if the formula for a curve can be transformed into the general form of the catenary, y = a * cosh(x/a), by making these substitutions, Y = ky and X = kx, then it's a catenary, too. Note that the same scaling factor, k, must be used for both X and Y.
Thanks, that makes sense. I should have figured that out myself, but I was overthinking it.
Quote: CrystalMathQuote: WizardQuote: ChesterDogThanks!
I did not know that sinh-1=ln[x+(1+x2)1/2].
And it's amazing to me that your (45 ln(40/9+Ā(1+(40/9)2 )1/2))/2 simplifies to 45ln3.
Good catch! I didn't know it simplified to that. Very elegant. For what it's worth, I chose the pole and rope length arbitrarily.
That is crazy. All the stuff inside the ln evaluates to 9, so we have 45*ln(9)/2, and ln(9)/2 = ln(3).
I checked to see if the simplification happens for other choices of rope length and maximum dip of the rope, and it does. If we let r = half of the rope length and h = maximum dip of the rope, then a formula for the distance, D, between the supports is:
D = ( 1 / h ) * ( r + h ) * ( r - h ) * ln[ ( r + h ) / ( r - h ) ]
Quote: AxelWolfDoes it matter how thick the rope is? I have to asuume that will make a difference? I have to assume all calculations are done without factoring in the thickness of the rope?
I'm sure the thickness of the rope would matter in the real world. Also, the elasticity of the rope and the attachments of the rope's ends would matter.
We have only been dealing with the ideal catenary.
Quote: AxelWolfDoes it matter how thick the rope is? I have to asuume that will make a difference? I have to assume all calculations are done without factoring in the thickness of the rope?
It assume thickness and weight of the rope is not an issue. Perhaps I should have said a string or the type of chain they use to secure pens at the bank (which never seem to have ink).
While I too have heard that girth matters, it appears that length trumps all, when it comes to the catenary position.Quote: AxelWolfDoes it matter how thick the rope is? I have to asuume that will make a difference? I have to assume all calculations are done without factoring in the thickness of the rope?
Quote: unJonWhile I too have heard that girth matters, it appears that length trumps all, when it comes to the catenary position.
I have heard girth is just as important, if not more.
If I am reading the problem correctly, the length of the rope isn't going to be 100.
Here's what I get:
The curve is f(x) = a cosh (x/a), with f(0) = 10 and f(d) = 50, where 2d is the distance between the poles.
f(0) = 10 = a cosh 0 = a -> a = 10 -> f(x) = 10 cosh (x/10)
f(d) = 50 = 10 cosh (d/10) -> 5 = cosh (d/10) -> d = 10 cosh-1 5
Excel says this is 22.9243, so the distance between the poles would be 45.8486
However, I am not sure if that value is in degrees or radians.
Thatís the answer I got as well.Quote: ThatDonGuyI tried to figure this one out, but something just doesn't make sense.
If I am reading the problem correctly, the length of the rope isn't going to be 100.
Here's what I get:
The curve is f(x) = a cosh (x/a), with f(0) = 10 and f(d) = 50, where 2d is the distance between the poles.
f(0) = 10 = a cosh 0 = a -> a = 10 -> f(x) = 10 cosh (x/10)
f(d) = 50 = 10 cosh (d/10) -> 5 = cosh (d/10) -> d = 10 cosh-1 5
Excel says this is 22.9243, so the distance between the poles would be 45.8486
However, I am not sure if that value is in degrees or radians.
Quote: ThatDonGuyI tried to figure this one out, but something just doesn't make sense.
If I am reading the problem correctly, the length of the rope isn't going to be 100.
Here's what I get:
The curve is f(x) = a cosh (x/a), with f(0) = 10 and f(d) = 50, where 2d is the distance between the poles.
f(0) = 10 = a cosh 0 = a -> a = 10 -> f(x) = 10 cosh (x/10)
f(d) = 50 = 10 cosh (d/10) -> 5 = cosh (d/10) -> d = 10 cosh-1 5
Excel says this is 22.9243, so the distance between the poles would be 45.8486
However, I am not sure if that value is in degrees or radians.
Here's the Wizard original question:
Quote: WizardA 100 meter rope is suspended from the top of two 50-meter poles. The lowest point of the rope is 10 meters from the ground. How far apart are the poles?...
Here's a hint on how to check your solution: If you change the 50-meter poles to 40-meter poles, the lowest point of the rope would then be tangent to the ground. But the distance between the poles would remain the same. When we solve this problem, the answer should be the same as for the 50-meter poles.
Quote: ChesterDogHere's a hint on how to check your solution: If you change the 50-meter poles to 40-meter poles, the lowest point of the rope would then be tangent to the ground. But the distance between the poles would remain the same. When we solve this problem, the answer should be the same as for the 50-meter poles.
That's another reason I'm pretty sure I'm going about it the wrong way; if I use f(x) = a cosh(x/a), but f(0) = 0, then a = 0 - but a can't be zero because then x/a is undefined.
Quote: ThatDonGuyThat's another reason I'm pretty sure I'm going about it the wrong way; if I use f(x) = a cosh(x/a), but f(0) = 0, then a = 0 - but a can't be zero because then x/a is undefined.
The Wizard gave us the general equation for a catenary as y = a cosh(x/a) - a. You can see that this is the equation for the catenary when it is tangent to the ground since when x = 0, then y = 0.
I worked on the problem many hours before giving up and Googling. The solution is so obvious to me in hindsight.
f(x) = a cosh(x/a) - a
f'(x) = sinh(x/a)
Let 2d be the distance between the poles; the rope goes through (0,0) and (d,40)
f(0) = 0
a (cosh (d/a) - 1) = 40
a cosh (d/a) = 40 + a
a2 cosh2 (d/a) = a2 + 80a + 1600
a2 (cosh2 (d/a) - 1) = 80a + 1600
a2 sinh2 (d/a) = 80a + 1600
50 = INTEGRAL(0,d) {sqrt(1 + sinh2(x/a)) dx}
50 = a INTEGRAL(0,d) {cosh(x/a)) d(x/a)}
50 = a INTEGRAL(0,d/a) {cosh t dt}
50 = a sinh (d/a)
2500 = a2 sinh2 (d/a)
Thus 80a + 1600 = 2500 -> a = 45/4
45/4 cosh (4d/45) = 205/4
cosh (4/45 d) = 205/45 = 41/9
d = 45/4 cosh-1 41/9
Distance between poles = 2d = 49.4376
Quote: ThatDonGuyIn that case...
f(x) = a cosh(x/a) - a
f'(x) = sinh(x/a)
Let 2d be the distance between the poles; the rope goes through (0,0) and (d,40)
f(0) = 0
a (cosh (d/a) - 1) = 40
a cosh (d/a) = 40 + a
a2 cosh2 (d/a) = a2 + 80a + 1600
a2 (cosh2 (d/a) - 1) = 80a + 1600
a2 sinh2 (d/a) = 80a + 1600
50 = INTEGRAL(0,d) {sqrt(1 + sinh2(x/a)) dx}
50 = a INTEGRAL(0,d) {cosh(x/a)) d(x/a)}
50 = a INTEGRAL(0,d/a) {cosh t dt}
50 = a sinh (d/a)
2500 = a2 sinh2 (d/a)
Thus 80a + 1600 = 2500 -> a = 45/4
45/4 cosh (4d/45) = 205/4
cosh (4/45 d) = 205/45 = 41/9
d = 45/4 cosh-1 41/9
Distance between poles = 2d = 49.4376
Nice! That agrees with CrystalMath's answer.


